DOĞRUSAL PROGRAMLAMA MODELLERİNİN ÇÖZÜMÜ: GRAFİK ÇÖZÜM TEKNİĞİ
Grafik çözümünde "uygun çözüm" ve "uygun çözüm alanı" nedir?
Bir doğrusal programlama modelinin tüm kısıtlarını sağlayan her X vektörüne,
X=[X1,X2, … Xj, … Xn] uygun çözüm denir.
Uygun çözümlerin oluşturduğu kümeye, Uygun Çözüm Alanı (UÇA) denir. Uygun Çözün Alanı={X | AX≤b, X≥0 }
Dışbükey alanın temel özelliği nedir?
Uygun Çözüm Alanı dışbükey(konveks) bir alandır. Dışbükey alanın temel özelliği, bu alan içinde iki nokta ele alınıp bir doğru parçasıyla birleştirildiğinde, birleştiren doğru parçasının tamamının alan kalmasıdır.
Amaç fonksiyonu maksimizasyon (en büyükleme) veya minimizasyon (en küçükleme) yönünde olan bir doğrusal programlama modelinin özellikleri nelerdir?
Amaç fonksiyonu maksimizasyon (en büyükleme) veya minimizasyon (en küçükleme) yönünde olan bir doğrusal programlama modelinin:
i. Eğer modelin optimum (en iyi) çözümü varsa, bu çözüm Uygun Çözüm Alanının bir köşe noktasındadır.
ii. Amaç fonksiyonu optimum (en iyi) değerini birden çok köşe noktasında alıyorsa, bu noktaların her dışbükey birleşimi de optimum(en iyi) çözümdür.
Doğrusal programlama modelinin grafik çözümünde yapılacak işlemler nelerdir?
i. Her bir kısıt eşitlik olarak ele alınıp, karşı gelen doğrunun grafiği çizilerek, kısıtı sağlayan yönü (bölge) işaretlenir. Tüm kısıtları aynı anda sağlayan bölge taranarak “Uygun Çözüm Alanı(UÇA)” olarak belirlenir.
ii. Uygun Çözüm Alanının köşe noktalarında karar değişkenlerinin ve amaç fonksiyonunun değeri hesaplanarak amacı sağlayan köşe, optimum çözüm noktası olarak ilan edilir.
iii. Optimum çözüm seti (amaç fonksiyonu ve karar değişkenlerinin değeri) yazılarak çözüme ulaşılmış olur.
Kısıtlayıcıların Grafik Çizimi yapılırken dikkat edilecek hususlar nelerdir?
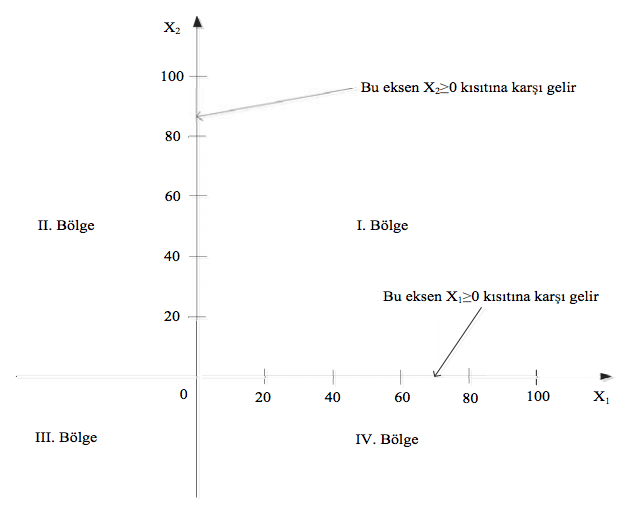
Doğrusal karar modelinin optimum çözümünü bulmak için öncelikle Uygun Çözüm Alanının(UÇA) belirlenmesi gerekmektedir. İlk adımda modelin kısıtlayıcıları olan doğrusal eşitsizliklerin grafiğini çizmek gerekir. Bütün doğrusal programlama modellerinde negatif olmama kısıtlayıcıları (X1, X2≥ 0) bulunduğundan, öncelikle bu kısıtların doyurulması ile başlamak gerekir. Koordinatlar ekseninde, uygun çözüm alanının hangi bölümde yer aldığı belirlenir. Örnek modeldeki X1(Ürün I’den üretilecek miktar) genellikle apsis (yatay) ekseninde, X2(Ürün II’den üretilecek miktar), ordinat (düşey) ekseninde gösterilir.
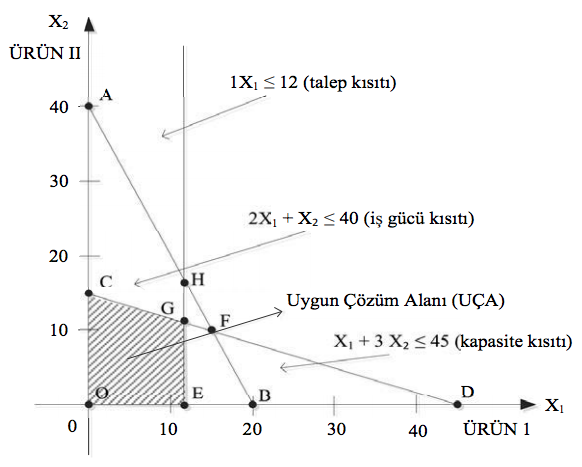
Uygun Çözüm Alanını nasıl belirlenmektedir?
Uygun Çözüm Alanının sınırları, kısıtlayıcı doğrusal denklemlerle ifade edilen, çizilen doğrusal eşitsizliklerin grafiği ile belirlenir. Karar modelinin tüm kısıtlayıcıları aynı düzlemde(I. Bölge) çizilerek, her bir kısıtın uygun alanları taranırsa, Uygun Çözüm Alanı (UÇA) taranmış bölge olarak ortaya çıkar.
Optimum (En İyi) Çözümün Bulunması sırasında, köşe noktaların X1 ve X2 değerlerini bulmak için ne yapılmalıdır?
Köşe noktaların X1 ve X2 değerlerini bulmak için, o noktada kesişen doğru denklemleri çözülür. Matematikten hatırlanacağı üzere, iki bilinmeyenli iki denklem çözümü ile X1 ve X2 değerleri kolayca bulunabilir.
Bir doğrusal karar modelinin çözümü, grafik çözüm tekniği ile araştırılırken hangi özel durumlar ile karşılaşılabilir?
Bir doğrusal karar modelinin çözümü, grafik çözüm tekniği ile araştırılırken bazı özel durumlardan birisiyle karşılaşılabilir.
1. Uygun çözüm alanı boş(uygun çözüm bulunmama),
2. Sınırsız Çözüm(amaç fonksiyonu uygun çözüm alanında sınırsız),
3. Seçenekli(çoklu) optimal çözüm.
Karar modelinin kısıtlarının grafiği çizildiğinde, uygun çözüm alanı oluşmaması (boş) ne anlama gelir?
Karar modelinin kısıtlarının grafiği çizildiğinde, uygun çözüm alanı oluşmuyor (boş) ise, problemin çözümü yoktur denir. Uygun çözüm bulunmaması, problemin yapısından kaynaklanabileceği gibi, modelleme hataları da (bir kısıtlayıcının yönünün ters olması gibi) uygun çözüm alanının boş olmasına neden olabilmektedir.
Bazı doğrusal programlama modellerinin amaç fonksiyonu değeri, uygun çözüm alanı üzerinde istenen yönde sonlu değilse, optimum değeri bulunamayacağından _____ vardır denir.
Yukarıdaki boşluğa hangi ifade gelmelidir?
Bazı doğrusal programlama modellerinin amaç fonksiyonu değeri, uygun çözüm alanı üzerinde istenen yönde sonlu değilse, optimum değeri bulunamayacağından, sınırsız çözüm vardır denir. Bu durum karar vericiye hiçbir öneri getiremez. Sınırsız çözümün varlığı, grafik çözümde, grafik üzerinde kolaylıkla görülebilir.
Bir karar modelinin seçenekli (alternatif) çözümü vardır diyebilmek için hangi şartların oluşması gerekir?
Doğrusal programlama problemleri birden çok optimum çözüme sahip olabilir. Karar modelinin amaç fonksiyonunun optimum değeri, uygun çözüm alanında iki ayrı noktada aynı değeri alıyorsa, modelin seçenekli (alternatif) çözümü vardır denir.
Bir doğrusal programlama problemini matematiksel modelle ifade etmenin avantajları nelerdir?
Bir doğrusal programlama problemini matematiksel modelle ifade etmek, en iyi çözümün araştırılmasının yanı sıra, problemin yapısında veya parametrelerde meydana gelebilecek değişiklikleri analiz etme imkanı da sağlar. Problemde iki karar değişkeni var ise, grafik çözümle tüm olası durumlar görülebilmekte ve analizler yapılabilmektedir.
Optimum (en iyi) çözüm seti ve e optimum (en iyi) değer nasıl tanımlanmaktadır?
Uygun Çözüm Alanı üzerinde Xj’lere göre, amaç fonksiyonunun maksimum (en büyük) veya minimum (en küçük) değerini aldığı Xj’lere optimum (en iyi) çözüm seti, amaç fonksiyonuna karşı gelen değerine optimum (en iyi) değer denir.
Dışbükey ve içbükey alanların arasındaki fark nedir?
Dışbükey alanın temel özelliği, bu alan içinde iki nokta ele alınıp bir doğru parçasıyla birleştirildiğinde, birleştiren doğru parçasının tamamının alan kalmasıdır. Bir anlamda Uygun Çözüm Alanı kümesindeki herhangi iki nokta çiftini birleştiren doğru parçası, tamamen Uygun Çözüm Alanı kümesinde ise, uygun çözüm alanı dışbükey bir kümedir. Söz konusu doğru parçasının bir kısmını içine almayan küme ise, içbükey (konkav) kümedir.
Uç(köşe) Nokta Teoremi'ni açıklayınız.
Uç(köşe) Nokta Teoremi: Grafik üzerinde Uygun Çözüm Alanının (UÇA) farklı iki noktasının dışbükey birleşimi olarak yazılamayan noktası varsa, buna uç nokta veya köşe nokta denir. Düzlemde bir üçgenin, bir karenin köşeleri uç (köşe) noktadır. Şu halde, amaç fonksiyonu maksimizasyon (en büyükleme) veya minimizasyon (en küçükleme) yönünde olan bir doğrusal programlama modelinin:
i. Eğer modelin optimum (en iyi) çözümü varsa, bu çözüm Uygun Çözüm Alanının bir köşe noktasındadır.
ii. Amaç fonksiyonu optimum (en iyi) değerini birden çok köşe noktasında alıyorsa, bu noktaların her dışbükey birleşimi de optimum(en iyi) çözümdür.
Aşağıdaki grafiğin karar modelini yazınız.
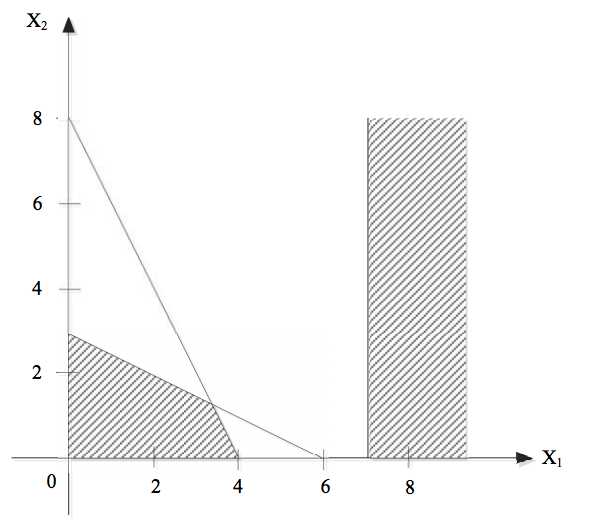
X1 + 2X2 ≤ 6
2X1 + X2 ≤ 8
X1 ≥ 7
ve X1, X2 ≥ 0
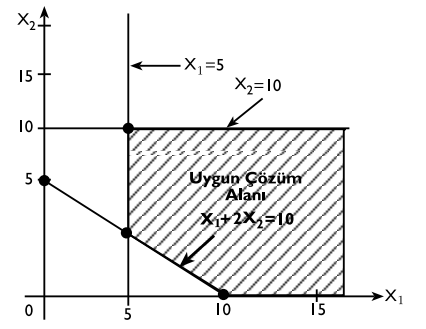
Aşağıdaki örnek problem karar modelinin uygun çözüm alanını grafikle gösteriniz.
Max Z = 3X1 + 5X2
Kısıtlayıcılar:
X1 ≥ 5
X2≤ 10
X1 + 2X2 ≥ 10
ve X1, X2 ≥ 0
8X1 + 6 X2≤ 24 kısıtının grafiği nasıl çizilmelidir?
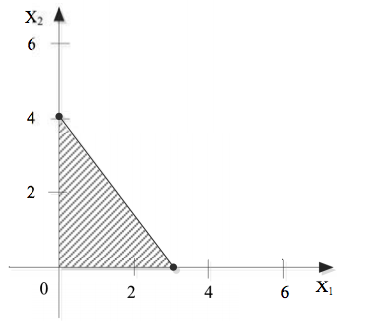
Grafik çözümde Uygun Çözüm Alanı koordinat sisteminin hangi bölgesinde yer alır?
Grafik çözümde Uygun Çözüm Alanı koordinat sisteminin I. bölgesinde yer alır.
Doğrusal programlama modelinin grafiği, koordinat diyagramının neden I. Bölge’sinde çizilir?
X1, ve X2 değişkenlerinin çözüm değerlerinin anlamlı olabilmesi için, negatif olmayan değer almaları gerekir. Yani X1≥0 ve X2≥0 koşulları sağlanmalıdır. İlgili üründen üretilecek ise, X1 pozitif bir değer alır; üretilmeyecek ise sıfır değerini alacak demektir. İlgili üründen üretilecek ise, X2 pozitif bir değer alır; üretilmeyecek ise sıfır değerini alacak demektir. Bunun yanında X1≥ 0, yatay eksenin(apsis) üst tarafını, X2≥ 0 düşey eksenin (ordinat) sağ tarafını işaret eder ki, bu da koordinat ekseninin I.Bölgesidir.