Benzerlik ve Uzaklık Ölçüleri

Genel bir tanımı olmamasına rağmen, iki nesne arasındaki benzerlik, iki nesnenin birbirine benzeme derecesinin sayısal bir ölçüsü olarak tanımlanabilir. Veri madenciliği çerçevesinde ise benzerlik genellikle nesnelerin özelliklerini temsil eden boyutlara sahip bir uzaklık olarak tanımlanabilir. Dolayısıyla, benzerlikler birbirine daha çok benzeyen nesne çiftleri için daha yüksektir.

Benzerlikler temel olarak [-1,1] arasında bir sayısal değer ile ifade edilebilmelerine rağmen, genellikle normalleştirilerek [0,1] arasında ölçeklendirilirler. Bu durumda “0” nesneler arasında hiç benzerliğin olmadığını, “1” ise ilgili nesnelerin tam benzer olduklarını, bir diğer ifadeyle aynı (özdeş) nesneler olduklarını ifade eder.

İki nesne arasındaki düzensizliğin veya bozukluğun bir ölçüsü olan uzaklık, farklılığın özel bir sınıfı, alt kümesidir.

Çoğunlukla, uzaklık kavramı farklılık kavramının yerine kullanılmasına rağmen aslında uzaklık, farklılıkların özel bir sınıfını ifade etmek için kullanılır. Farklılık, çeşitli özelliklere dayalı olarak iki nesne arasındaki zıtlık ya da uyumsuzlukların bir ölçümü olarak nitelendiğinde, uzaklık iki nesne arasındaki düzensizliğin veya bozukluğun bir ölçüsü olarak düşünülebilir. Kısaca uzaklık ölçüleri yardımıyla iki nesne arasındaki farklılığın derecesi ölçülmektedir. Dolayısıyla, birbirine benzemeyen nesne çiftleri için farklılıklar fazla ve uzaklık ölçüsünün alacağı değer de o oranda büyük olurken birbirine daha çok benzeyen nesne çiftleri için farklılıklar daha az ve uzaklık ölçüsünün alacağı değer de o oranda küçük olacaktır. Farklılıklar kimi zaman [0,1] aralığına düşecek şekilde tanımlansa da genel olarak [0,∞) aralığındadır.

X bir küme olmak üzere d: X x X ⟶ ℜ şeklinde tanımlanan bir fonksiyon, tüm x, y ∈ X için;

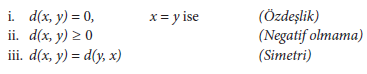
koşullarını sağlıyorsa d, X üzerinde bir uzaklık olarak adlandırılır. Bu koşullara ilave olarak eğer tüm x, y, k ∈ X için;

koşulu da sağlanıyor ise d, X üzerinde metrik uzaklık olarak adlandırılır.

X bir küme olmak üzere s: X x X ⟶ ℜ şeklinde tanımlanan bir fonksiyon, tüm x, y ∈ X için;

koşullarını sağlıyorsa s, X üzerinde benzerlik olarak adlandırılır.

Hesaplamalar sonucunda elde edilen benzerlik değeri arttıkça iki nesne arasındaki benzerliğin de arttığı anlaşılırken bunun tam tersine elde edilen uzaklık değeri azaldıkça bu iki nesne arasındaki benzerliğin arttığı anlaşılmaktadır.

Bu ifadelerden yola çıkarak iki nesne arasındaki benzerlik s(x, y) olarak tanımlandığında, ilgili iki nesne arasındaki uzaklık d(x, y) = 1 – s(x, y) olarak tanımlanır. Veri madenciliği çalışmalarında benzerlik ve uzaklık kavramlarının ortak ifadesi olarak yakınlık ifadesi de kullanılmaktadır.

Dönüşümler genellikle benzerlik ve uzaklıklara ilişkin ölçüm değerlerinin birbirlerine dönüştürülmesinde veya her ikisi için farklı aralıklarda elde edilmiş ölçüm değerlerinin [0,1] gibi belirli bir aralık içerisinde ölçeklendirilmesi amacıyla kullanılırlar.

Birçok veri madenciliği uygulamasında özellikle benzerlik ölçüm değerlerinin [0,1] aralığında tanımlanmış veya bu aralıktaki değerlere dönüştürülmüş olması beklenir. Sonlu bir aralıkta değerler alan benzerlik ölçüm değerleri [0,1] aralığına uyacak şekilde dönüştürülmek istendiğinde,

eşitliğinden yararlanılır. Eşitlik yardımıyla elde edilecek s’ değeri, dönüştürülmesi istenilen s benzerlik ölçüm değerinin [0,1] aralığına düşen değerini ifade eder.

Uzaklık ölçüm değerleri [0,1] aralığına uyacak şekilde dönüştürülmek istenebilir. Bu durumda ise,

eşitliğinden yararlanılır. Burada elde edilecek d’ değeri, dönüştürülmesi istenilen d uzaklık değerinin [0,1] aralığına düşen değerini ifade eder.

Yakınlık ölçüm değerleri her zaman sonlu aralıkta olmayabilir. Yakınlık
ölçüm değerleri genellikle matematiksel olarak [0,∞) aralığında değerler almaktadırlar. Bu durumda yakınlık ölçüm değerlerini [0,1] sonlu aralığında ifade etmek için doğrusal olmayan bir dönüşüm uygulanır. Örnek olarak [0,∞) aralığında değerler alan bir uzaklık ölçümü için,

eşitliği yardımıyla ölçüm değerleri [0,1] sonlu aralığına dönüştürülmüş olur.

Benzerlik ve uzaklık değerleri arasındaki geçişlerde ölçüm değerlerinin sonlu aralıkta olup olmamasına göre iki farklı durum söz konusudur. Benzerlik değerlerinin [0,1] sonlu aralığında olduğu ilk durumda, ilgili uzaklık değerleri,

d=1-s

eşitliği yardımıyla elde edilebilir.Aynı şekilde [0,1] kapalı aralığındaki uzaklık değerlerine karşı gelen benzerlik değerleri elde edilmek istendiğinde ise

s = 1 – d

eşitliğinden faydalanılır. [0,1] kapalı aralığında tanımlanmış benzerlik ve uzaklık değerleri, toplamları 1 olan yakınlık ölçüleridir. İkinci durum ise yakınlık değerlerinin sonlu aralıkta ölçümlenmemiş olma durumudur. Örneğin bir araştırmada elde edilen uzaklık değerleri [0,∞) aralığında değerler alıyor iken istenilen benzerlik değerlerini elde edebilmek için,

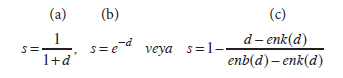
eşitliklerinden faydalanılır. Aslında benzerlik ve uzaklık değerlerinin birbirlerine dönüşümü için herhangi bir monoton azalan fonksiyon da kullanılabilir. Ancak bu dönüşümler yapılırken probleme özgü diğer faktörlerin de göz önünde bulundurulmasında yarar vardır.

Bir dizi niteliğe sahip nesnelerin yakınlığı, nesnelerin her bir niteliği için elde edilecek yakınlıklarının birleşimi olarak tanımlanır.

Sıralayıcı nitelik bakımından iki nesne karşılaştırıldığında durum biraz daha karmaşıklaşır. Örneğin bir araştırmada üretilen bir ürünün kalitesinin {kötü, zayıf, orta, iyi, mükemmel} olarak değerlendirildiğini varsayalım. Bu şekilde nitelendirilen iki ürünün benzerliklerini ölçmek için ilk olarak niteliğin her bir sonucuna 0 veya 1’den başlamak suretiyle {kötü = 0, zayıf = 1, orta = 2, iyi = 3, mükemmel = 4} şeklinde tamsayı değerler atanır. İlgilenilen niteliğin ortaya çıkış biçimleri bu şekilde tam sayı değerlerle ifade edildikten sonra, nesneler arası uzaklık değeri

d(x, y) = |x – y|

eşitliği yardımıyla elde edilir. Elde edilen uzaklık değeri [0,1] aralığında değer alacak biçimde dönüştürülmek istendiğinde ise

d(x, y) = |x – y| / (n –1)

eşitliği kullanılır. Eşitlikte n, niteliğin ortaya çıktığı sonuç sayısıdır. Dönüşümler konusunda ele alındığı üzere, uzaklık değeri yardımıyla benzerlik değeri

s(x, y) = 1 – d

eşitliği yardımıyla hesaplanır.

Birim ya da değişkenler arası benzerlik ya da uzaklık değerleri hesaplanırken geometrik yaklaşımlardan yararlanılır.

Geometride koordinat sistemindeki iki nokta arasındaki en yakın uzaklık Pisagor bağıntısına göre elde edilir. Dolayısıyla koordinat sisteminde yer alan A ve B noktaları arasındaki doğrusal uzaklık, A noktasının koordinat değerleri A(x₁, y₁) ve B noktasının koordinat değerleri B(x₂, y₂) olmak üzere Pisagor bağıntısına göre;

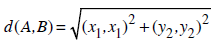
eşitliği yardımıyla hesaplanır (S:81, Şekil 4.1).

Yakınlık ölçüleri, temel olarak ilgilenilen değişkenlerin nicel (sayısal) veya nitel (kategorik) olmasına göre farklılık gösterir. Değişkenlerin bu şekilde sınıflandırılmasının nedeni ise, değişkenlere ilişkin ölçüm değerlerinin matematiksel özelliklerine göre sınıflayıcı, sıralayıcı, aralıklı ve oransal olmak üzere dört ölçek ile ölçülmesidir. 

Uzaklık ölçüleri arasında en yaygın kullanılan uzaklık ölçüleri Öklid ve Karesel Öklid uzaklık ölçüleridir. Her biri p tane nicel değişken içeren x_i ve x_j nesneleri arasındaki Öklid uzaklığı,

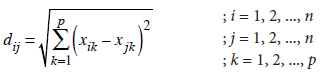
eşitliği yardımıyla hesaplanır. Eşitlikte,
n : nesne sayısını
p : değişken sayısını
d_ij : i’nci ve j’inci nesneler arasındaki uzaklığı
x_ik : i’inci nesnenin k’ıncı değişkendeki değerini
x_jk : j’inci nesnenin k’ıncı değişkendeki değerini

ifade eder.

Öklid uzaklığı, i’inci ve j’inci nesnelerin p tane değişken için farklarının kareleri toplamının karekökü alınarak elde edilir. Öklid uzaklığı hesaplanırken veriler kullanılır. Dolayısıyla farklı ölçekler ve değişkenlerin farklı ölçü birimleri ile ölçülmüş olması, hesaplanacak uzaklık değerini etkileyecektir.

Öklid uzaklık ölçüsü, değişkenlerin birbirinden bağımsız olduklarını varsayar. Aynı zamanda L₂ norm olarak da bilinen Öklid uzaklığının hesaplanabilmesi için verilerin oransal ya da aralıklı ölçekle ölçülmüş olması gerekir. Öklid uzaklığı “sıfır” ile “sonsuz” arasında değerler alır yani tanım aralığı [0,∞)’dur.

Karesel Öklid uzaklığı ise Öklid uzaklığına benzer biçimde hesaplanır. Tek farkı değişkenlere göre toplam uzaklığın karekök alınmadan hesaplanmasıdır. Yani Öklid uzaklığının karesidir.

Karesel Öklid uzaklığının hesabında karekök alınmadığından Öklid uzaklığına göre veri kümesi içerisinde yer alan aykırı değerlere (outliers) daha fazla ağırlık verme eğilimindedir. Aykırı değerler veri kümesinin genel özelliklerinden belirgin bir şekilde farklılık gösteren gözlem değerleridir. Bu farklılıkların analizler üzerinde etki gösterip göstermeyeceğine ilişkin karar araştırmacı tarafından verildikten sonra ilgili uzaklık ölçüsü hesaplanmalıdır.

R ile Öklid uzaklığı hesaplayabilmek için R’nin temel paketlerinden stats paketinde yer alan dist() fonksiyonundan yararlanılır. Her ne kadar R yazılımı çalıştırıldığında ilgili pa­ket otomatik olarak yükleniyor olsa da R’nin komut satırından library (stats) komutunun verilmesi ile paketin kullanıma hazır hale getirilmesi gerekebilir.

dist() fonksiyonu yardımıyla veri matrisi olarak girilen x değişkenine ait nesneler ara­sındaki belirli uzaklık ölçüm değerleri hesaplanabilir. dist() fonksiyonunun temel para­metreleri, veri matrisini ifade eden x ve hesaplanmak istenen uzaklık ölçüsü yöntemi­nin seçimini sağlayan method parametreleridir. Bu fonksiyon ile ilgili yardım için, help (“dist”) komutundan yararlanılabilir.

Karl Pearson uzaklığı, Öklid uzaklığının değişkenin varyansına oranlanması ile elde edilen bir uzaklıktır. Bu özelliğinden dolayı standartlaştırılmış Öklid uzaklığı olarak da bilinmektedir. Öklid uzaklığı yaygın olarak tercih edilen bir uzaklık ölçüsü olmasına rağmen, değişkenlerin ölçü birimlerinden kolaylıkla etkilenmektedir. Dolayısıyla farklı ölçü birimlerine sahip değişkenler söz konusu olduğunda hesaplama yapmadan önce değişkenlerin standartlaştırılması gerekir. böyle bir durumda ölçü birimi farklılıklarını ortadan kaldırmak amacıyla Öklid uzaklığının standartlaştırılmış şekli olan Karl Pearson uzaklığı,

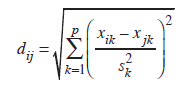
eşitliği yardımıyla hesaplanır. Eşitlikte s_k², k’ıncı değişkenin varyans değeridir. Öklid uzaklığının herbir değişkenin varyansı ile ağırlıklandırılması şeklinde hesaplanan Karl Pearson uzaklığı yardımıyla, büyük varyansa sahip değişkenlere, küçük varyansa sahip değişkenlere göre daha az ağırlık verilmektedir.

Manhattan (City Block) uzaklığı, birimler arası farkların mutlak değerinin toplamı alınmak suretiyle

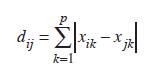
eşitliği yardımıyla hesaplanmaktadır. Aynı zamanda L1 norm olarak da bilinen Manhattan uzaklığı bir başka uzaklık ölçüsü olan Minkowski uzaklığının özel bir hâlidir. Manhattan uzaklığı, değişkenler arasında ilişki olmaması durumunda hesaplanması gereken bir uzaklık ölçüsüdür. Ayrıca Manhattan uzaklığının aykırı değerlere karşı hassasiyeti düşüktür.

Diğer uzaklıklara nazaran hesaplanması kolay olan Manhattan (City-Block) uzaklığı, değişkenler arasında yüksek derecede ilişki olması durumunda veya değişkenlerin ölçü birimleri farklı olduğunda kullanılmamalıdır.

R ile Manhattan uzaklığı hesaplayabilmek için R’nin temel paketlerinden stats paketinde yer alan dist() fonksiyonundan yararlanılır.

n sayıda birim ve p sayıda değişken ile çalışılırken birimler yada değişkenler arasındaki uzaklıkları hesaplamak için kullanılan genel bir uzaklık ölçüsüdür. L_λ norm olarak da bilinen Minkowski uzaklığı,

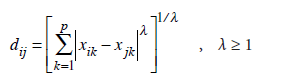
eşitliği yardımıyla hesaplanır. Minkowski uzaklık ölçüsündeki λ değeri büyük ve küçük farklara verilen ağırlığı değiştirir. Farklı λ değerleri için farklı uzaklık ölçüleri elde edilebileceği için genel uzaklık ölçüsü olarak nitelendirilir. Örneğin, λ = 1 olması durumunda Manhattan (City-Block) uzaklığı elde edilirken, λ = 2 olması durumunda ise Öklid uzaklığı elde edilmektedir.

R ile Minkowski uzaklığı hesaplayabilmek için R’nin temel paketlerinden stats paketinde yer alan dist() fonksiyonundan yararlanılır. Ancak Minkowski uzaklığını hesaplayabilmek için ayrıca bir p parametre değerinin girilmesi gerekmektedir. p parametresinin değeri aslında Minkowski uzaklık ölçüsünün kuvveti olan ve nesneler arası farklara verilen ağırlığı ifade eden λ değeridir.

Minkowski uzaklık değerlerini hesaplarken;

1. p = 1 alınması hâlinde Manhattan (City-Block) uzaklığı değerlerinin
2. p = 2 alınması hâlinde ise Öklid uzaklığı değerlerinin

elde edilebildiği komut dizileri izleyen yapıya sahiptir.

Doğrusal ilişki katsayısı olarak da bilinen Pearson korelasyon katsayısı, iki veya daha fazla ve en az aralıklı ölçeğe uygun şekilde ölçümlenmiş n adet gözlem içeren değişkenler arasındaki doğrusal ilişkinin yönünün ve derecesinin belirlenmesinde kullanılan bir katsayıdır ve r sembolü ile gösterilir. Aynı zamanda Pearson korelasyon katsayısı iki değişkenin gözlem değerleri arasındaki benzerliğin de bir ölçüsüdür.

Korelasyon katsayısının hesaplanabilmesi için değişkenlerin gözlem sayılarının eşit olması gerekmektedir. Dolayısıyla her biri n adet gözlem değeri içeren x ve y değişkenleri arasındaki benzerliği ortaya koymak amacıyla Pearson korelasyon katsayısı

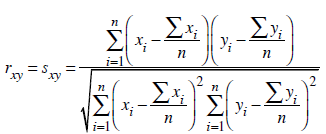
eşitliği yardımıyla hesaplanır.

Korelasyon katsayısı [-1,+1] arasında değerler alır. -1 ve +1 değerleri incelenen iki değişken arasında tam/mükemmel bir ilişkiyi ifade ederken, 0 (sıfır) değeri ilgili değişkenler arasında hiç ilişkinin olmadığını ifade eder. Hesaplanacak katsayı değerinin eksi işaretli olması değişkenler arasında ters yönlü bir ilişki olduğunun, artı işaretli olması ise değişkenler arasında aynı yönlü bir ilişki olduğunun göstergesidir.

Pearson korelasyon katsayısı, değişkenlerin gözlem değerlerinin kendi ortalamalarından farkları alınmak suretiyle standartlaştırıldığı açısal benzerlik ölçüsüdür.

Korelasyon uzaklığı ise bir benzerlik ölçüsü olarak ele alınan Pearson korelasyon katsayısından yararlanarak, değişkenler arasındaki uzaklığı hesaplayan ve sürekli değişkenler için yaygın olarak kullanılan bir uzaklık ölçüsüdür. Korelasyon uzaklığı Pearson korelasyon katsayısını temel alarak hesaplandığı için iki değişkenin öznitelik değerleri arasındaki doğrusal ilişkinin yönü ve gücünün belirlenmesinde kullanılan bir uzaklık ölçüsüdür. Korelasyon uzaklığı

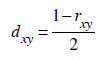
eşitliği yardımıyla elde edilir. Her ne kadar Pearson korelasyon katsayısı [-1,+1] arasında değerler alsa da korelasyon uzaklığının değerleri [0,1] aralığında değerler almaktadır.

R ile Pearson Korelasyon katsayısını hesaplayabilmek için R’nin temel paketlerinden stats paketinde yer alan cor() fonksiyonundan yararlanılır.

cor() fonksiyonu yardımıyla her biri n adet gözlem değeri içeren x ve y değişkenleri sütun vektörleri arasındaki Pearson korelasyon katsayısı hesaplanır. cor() fonksiyonunun temel parametreleri, değişkenlerin gözlem değerleri vektörleri x ve y ile hesaplanmak istenen korelasyon katsayısı tipinin seçimi için method parametreleridir. Şayet method parametresi için herhangi bir atama yapılmazsa varsayılan olarak Pearson korelasyon katsayısı hesaplanır. Bu fonksiyon ile ilgili yardım için, help(“cor”) komutundan yararlanılabilir.

Açısal benzerlik, iki vektör arasındaki açı farkının kosinüsünün bu iki vektör arasındaki uzaklık olarak alınması suretiyle değişkenler arasındaki benzerliğin belirlenmesine yönelik bir benzerlik ölçüsüdür. İki vektör arasındaki açı farkı sıfır olduğunda yani vektörler birbirlerine paralel olduklarında kosinüs değeri 1 olurken bu iki vektör arasındaki açı farkı 90° olduğunda yani vektörler birbirlerine dik olduklarında kosinüs değeri 0 olur. Dolayısıyla elde edilen değerin 1 olması değişkenler arasında tam bir benzerliğin olduğunun, 0 olması ise değişkenlerin hiç benzerliğin olmadığının göstergesi olmaktadır.

Açısal benzerlik, özellikle belge ve çoklu ortam nesnelerinin kıyaslanmasında ve metin madenciliğinde kullanılmaktadır.

x ve y birer vektör olmak üzere, bu iki vektör arasındaki açının kosinüsü, dolayısıyla açısal benzerliği,

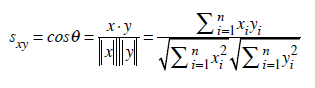
eşitliği yardımıyla hesaplanır. Eşitlikte yer alan “x . y” ifadesi x ve y vektörlerinin nokta (skaler) çarpımını ifade etmektedir. Açısal benzerlik ölçütü [-1,1] aralığında değerler alır.

ile Açısal Benzerlik (Cosine Similarity) değerini hesaplayabilmek için lsa paketinde yer alan cosine() fonksiyonundan yararlanılır. Dolayısıyla hesaplamalardan önce library(lsa) komutu ile paketin R’de kullanıma hazır hâle getirilmesi gerekir.

lsa paketi içerisinde yer alan cosine() fonksiyonu yardımıyla her biri n adet gözlem değeri içeren x ve y değişkenleri sütun vektörleri arasındaki açının kosinüsü, yani açısal benzerliği hesaplanır. cosine() fonksiyonunun temel parametreleri, veri vektörleri olan x ve y parametreleridir. Bu fonksiyon ile ilgili yardım için, help(“cosine”) komutundan yararlanılabilir.

Sürekli değişkenler arasındaki yakınlığın belirlenmesinde kullanılan bir diğer ölçü ise Mahalanobis uzaklığıdır. Bu uzaklık ölçüsü, iki vektör veya değişken arasındaki uzaklığın belirlenmesinde verilerin kovaryans yapılarını da dikkate almaktadır. Her biri n boyutlu x ve y gözlem vektörleri arasındaki Mahalanobis uzaklığı,

eşitliği yardımıyla hesaplanır. Burada S, n × n boyutlu örneklem ya da küme içi kovaryans matrisidir. Temel olarak bir nesnenin D dağılımının ortalamasından kaç standart sapma uzaklıkta olduğu araştırılmaktadır. Eğer ilgili nesne D’nin ortalamasında ise bu uzaklık doğal olarak sıfır olacaktır.

Mahalanobis uzaklığının hesaplanabilmesi için öncelikle S örneklem kovaryans matrisinin tersi olan S^–1 matrisinin elde edilmesi gerekir. Kimi durumlarda S^–1 matrisini elde etmede sorun yaşanabilir. Şayet değişkenler arasında bir ilişki söz konusu değilse örneklem kovaryans matrisi S, birim matris yapısına sahip olur ki bu durumda Mahalanobis uzaklığı Öklid uzaklığına eşdeğer olur. Mahalanobis uzaklığı veri madenciliğinde özellikle kümeleme analizi ile sınıflama çalışmalarında sıklıkla kullanılmaktadır. Ek olarak ilgilenilen veri kümesi içerisinde aykırı değerlerin varlığını araştırmak için de Mahalanobis uzaklığından faydalanılır.

Mahalanobis uzaklığının R ile hesaplanabilmesi için stats paketi içerisinde yer alan mahalanobis() fonksiyonu kullanılmaktadır.

mahalanobis() fonksiyonun temel parametreleri, uzaklık değerleri hesaplanmak istenen değerler vektörünü ifade eden x, dağılımın ortalama vektörü olan center ve örneklem kovaryans matrisini ifade eden cov parametreleridir. Bu fonksiyon ile ilgili yardım için, help(“mahalanobis”) komutundan yararlanılabilir.

İki sonuçlu (binary) değişkenler, ölçüm değerleri sınıflama yoluyla elde edilen nitel değişkenlerdir. Bu değişkenler sadece evet/hayır, var/yok, erkek/kadın, doğru/yanlış gibi değerler alırlar.

İki sonuçlu değişkenler için benzerlik veya uzaklık ölçüm değerlerin hesaplanabilmesi için her bir nesne incelenen değişkenlere ilişkin aldığı değerlerden oluşan bir vektör şeklinde ifade edilir. İki sonuçlu değişkenler içeren gözlem çiftleri arasındaki yakınlığın belirlenmesinde Öklid, Karesel Öklid, Büyüklük Farkı (Size Difference), Örüntü Farkı (Pattern Difference), Lance ve Williams Uzaklık Ölçüsü, Biçim Farkı (Shape Difference) ve Jaccard Benzerliği (Jaccard Similarity) gibi birçok benzerlik ya da uzaklık ölçülerinden yararlanılmaktadır.

Bu ölçüler temel olarak eşleştirmeye dayanan ölçüler olduklarından, hesaplama yapmadan önce kontenjans ya da diğer adıyla çapraz sınıflama tablosunun oluşturulması gerekir. İki yönlü sınıflama tablosu olarak da adlandırılan kontenjans tablosu, iki sonuçlu değişkenler içeren nesne çiftinin karşılıklı eşleşen değerlerinin tekrar sayılarından oluşan tablodur. Kontenjans tablosunda herhangi bir değişkenin varlığı “1” ya da “+” ile, yokluğu ise “0” ya da “–” ile gösterilir. Buna göre iki sonuçlu nesne çifti için düzenlenen kontenjans tablosu (S: 93, Tablo 4.5)’de verilmiştir. Burada,

a değeri: i ve j nesnelerinin her ikisinde de ilgilenilen değişkenin olmadığı yani yok olduğu durum (0-0 eşleşmesi) sayısını,

b değeri: ilgilenilen değişkenin i nesnesinde var olduğu ve j nesnesinde olmadığı durum (1-0 eşleşmesi) sayısını,

c değeri: ilgilenilen değişkenin i nesnesinde olmadığı ve j nesnesinde var olduğu durum (0-1 eşleşmesi) sayısını,

d değeri: i ve j nesnelerinin her ikisinde de ilgilenilen değişkenin var olduğu durum (1-1 eşleşmesi) sayısını,

p değeri: değişken sayısını göstermektedir.

Basit eşleştirme katsayısı, p tane değişken açısından ilgilenilen nesnelerin her ikisinde de olmama (0-0) ve olma (1-1) durum sayılarının oranını gösteren bir benzerlik ölçüsüdür. Diğer bir anlatımla, tesadüfi olarak seçilen bir değişkende her iki nesnenin de aynı özelliğe sahip olma olasılığını veren bir katsayıdır. Basit eşleştirme katsayısı,

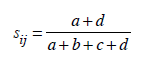
eşitliği ile hesaplanır. Bu katsayı [0,1] arasında değerler almakta ve üst sınır olan 1 değeri nesnelerin birbirlerine tam benzer olduğunu ifade etmektedir.

Basit eşleştirme katsayısından yola çıkılarak basit eşleştirme uzaklığı,

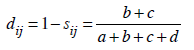
eşitliği yardımıyla elde edilir.

R ile Basit Eşleştirme Katsayısı değerini hesaplayabilmek için scrime paketinde yer alan smc() fonksiyonundan yararlanılır. Dolayısıyla hesaplamaları gerçekleştirebilmek için öncelikle library(scrime) komutu ile paketin R’de kullanıma hazır hale getirilmesi gerekir.

scrime paketi içerisinde yer alan smc() fonksiyonu yardımıyla iki sonuçlu değerler alan değişkenler arasındaki basit eşleştirme katsayısının değeri hesaplanır. smc() fonksiyonunun temel parametreleri, satırlarında nesnelerin ikili sonuçlarının girildiği veri matrisi x ve benzerlik veya uzaklık değerinden hangisinin hesaplanacağı seçimi için dist parametreleridir. Bu fonksiyon ile ilgili yardım için, help(“smc”) komutundan yararlanılabilir.

Binary Öklid uzaklığı, iki sonuçlu değişkenler arasındaki yakınlığın belirlenmesinde yaygın olarak kullanılan ve tutarlı bir ölçü olduğu kabul edilen bir uzaklık ölçüsüdür. Binary Öklid uzaklığı,

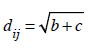
eşitliği yardımıyla hesaplanır.

Binary Karesel Öklid uzaklığı ise Binary Öklid uzaklığının karesi alınmak suretiyle elde edilir. Dolayısıyla Binary Karesel Öklid uzaklığı ise

eşitliği yardımıyla hesaplanır. Her iki uzaklık ölçüsü de iki nesnenin eşleşmeyen değişken sayıları üzerinden hesaplama yapılması mantığına dayanır. Hesaplanan ilgili uzaklıklar için elde edilecek değerler [0,∞) aralığında yer alacaktır.

R ile Binary Öklid uzaklığı değerini hesaplayabilmek için vegan paketinde yer alan vegdist() fonksiyonundan yararlanılır. Dolayısıyla işlemleri yapabilmek için önce library(vegan) komutu ile paketin R’de kullanıma hazır hâle getirilmesi gerekir.

vegan paketi içerisinde yer alan vegdist() fonksiyonu yardımıyla Binary Öklid uzaklığının değeri hesaplanır. vegdist() fonksiyonunun temel parametreleri, veri matrisini ifade eden x, hesaplanmak istenen uzaklık ölçüsü yöntemi seçimi için method ve veri tipini belirleyen binary parametreleridir. Bu fonksiyon ile ilgili yardım için, help(“vegdist”) komutundan yararlanılabilir.

Jaccard benzerlik katsayısı özellikle ekolojik araştırmalarda belirli bir nesnenin farklı bölgelerde var olup olmadığının belirlenmesinde kullanılmaktadır. İki nesnenin de araştırma bölgesi sınırları içerisinde var olmaması (0-0) durumu gözlem değeri sayısının (a’nın) göz ardı edildiği durumları dikkate alarak hesaplanan bir benzerlik ölçüsüdür. Buna göre Jaccard benzerlik katsayısı,

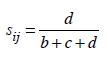
eşitliği yardımıyla hesaplanır. Jaccard benzerlik katsayısı [0,1] arasında değerler almaktadır. Jaccard benzerlik katsayısı ile elde edilecek Jaccard uzaklık değeri ise

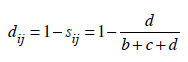
şeklinde elde edilir.

R ile Jaccard uzaklığı değerini hesaplayabilmek için vegan paketi içerisinde yer alan vegdist() fonksiyonundan yararlanılır. Bu amaçla vegdist fonksiyonu içerisinde method parametresine method = “jaccard” girişi yapılır.