Kinematik
Mekanik fiziksel bilimler içerisinde en eskiye dayanan alanlardan biri olup, genel olarak dinamik, statik ve kinematik olmak üzere üç farklı kavramla birlikte ele alınır. Bu üç alanın neleri incelediğini açıklayınız.
Dinamik hareket olayının, kuvvet ve kütle gibi kavramlarla ilişkilendirilmesini, statik cisimlerin denge durumlarını, kinematik ise hareketin nedenlerinden ziyade yer değiştirme, hız ve ivme gibi hareketi tanımlayıcı kavramlar arasındaki ilişkileri belirtmektedir.
Aşağıdaki şekle göre hareketli A noktasından başlayıp B, C ve D noktalarından geçerek dikdörtgen biçimindeki yolu takip edip başladığı yere yani A noktasına tekrar dönmüştür. Alınan yol ve yer değişimini açıklayınız.
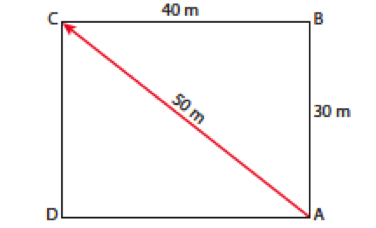
Bu durumda alınan toplam yol 30m+40m+30m+40m=140m iken hareketlinin yer değiştirmesi sıfırdır. Yani hareketli başladığı yere geri dönmüş olup, 140m yol almış olmasına karşın hiç yer değiştirmemiştir.
“Çok hızlı” ya da “çok yavaş” bunun gibi kavramları günlük yaşantımızda oldukça sık duyarız. Hız bize belirli bir olayın gerçekleşme süresi hakkında fikir vermektedir. Bu noktada hız ve sürat kavramlarının benzer ve farklı yönlerinin belirtiniz.
SI birim sisteminde hem hız hem de sürat için birim m/s ’dir. Bununla birlikte hız vektörel bir nicelik olup sürat ise skaler bir kavramdır. Ortalama hız hareketlinin yer değiştirmesine bağlı iken ortalama sürat ise alınan toplam yola bağlılık göstermektedir. Ortalama hız, bir boyutta;
vort = Δx Δt = x2 −x1 t 2 −t 1 ifadesiyle verilir.
Burada x2 hareketlinin x ekseni üzerindeki son konumu x1 ise ilk konumudur. t2-t1 ise hareketlinin son konumuna gelene kadar geçen süredir.
İvme nedir? Açıklayınız.
İvme bir hareketlinin hızındaki değişime bağlı olarak ortaya çıkmakta olup, bu değişim hızın büyüklüğünde olabileceği gibi sadece yönüyle veya hem yönüyle hem de büyüklüğüyle ilgili de olabilmektedir. SI birim sisteminde ivme için m/s2 birim olarak kullanılmaktadır. Bir boyutta, ivme hızdaki değişimin bir ölçüsüdür. Ortalama ivme, aort = Δv Δt = v2−v1 t ifadesiyle verilmektedir. Bu eşitlikte v2 hareketlinin son hızını, v1 başlangıç yani ilk hızını, t ise bu esnada geçen süreyi temsil etmektedir. İvme hız gibi yönlü olup vektörel bir niceliktir.
72 km/h’lik sabit bir hızla doğrusal bir yol üzerinde hareket eden bir araç 20 dakika süre içerisinde kaç metre yol alır?
Öncelikle 72 km/h ifadesini m/s cinsinden ifade etmek gerekmektedir. Burada bilinmesi gereken 1 km=1000 m ve 1 h=3600 s olduğudur. Bu durumda; 72 kmh = 72.1000 m, 3600 s = 20 ms olarak bulunur. Ayrıca 20 dakika=20x60 s=1200 s’ye karşılık gelmektedir. x =x0+vt hareket denkleminde, x0=0 alınırsa, yani başlangıç noktası sıfır olarak alınırsa, alınan yol; x = x0 + vt = 0+ 20 ms x 1200 s = 24000 m = 24 km olarak bulunur.
x ekseni üzerinde +x ekseni yönünde 20 m/s’lik sabit bir hızla x=5 m noktasından harekete başlayan bir cismin 8 s sonunda orijine olan uzaklığını bulunuz.
Burada cisim x0=5 m noktasından harekete başlamıştır yani daha hareketin başında orijine olan uzaklığı 5 m’dir. Bu durumda x=x0+vt olduğundan; x = 5 m + 20 ms x 8 s =165 m olarak bulunur. Aslında cisim 8 s boyunca 160 m yol almıştır. Başlangıçta orijine olan uzaklığı ise 5 m olduğundan, 8 s sonunda orijine olan uzaklığı 165 m olmuştur.
Düzgün değişen doğrusal hareket nedir?
Bir doğru boyunca ya da bir düzlem üzerinde doğrusal bir yol boyunca hareket eden cisimlerin zamanla hızlarında değişikliler söz konusu olabilir. Bu değişim sabit ivmeli gerçekleşiyor ise, başka bir değişle hareketlinin hızı belirli zaman aralıklarında eşit miktarlarda artıyor veya azalıyor ise bu harekete düzgün değişen doğrusal hareket denilmektedir. Bu harekette düzgün olarak değişen hızdır.
Durağan halden harekete başlayan bir araç doğrusal bir yol boyunca 4 m/s2 ivme ile 8 s boyunca hareket etmiştir. Bu aracın 8 s’de aldığı yolu ve ulaştığı son hızı bulunuz.
Aracın harekete başlangıç noktasını x0=0 seçelim. Yani araç orjinden harekete başlamış olsun. Araç durgun halden harekete başladığı için v0=0 olur. Bu durumda alınan yol;
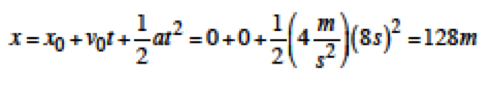
olarak bulunur. Bu örnekte aracın 8s sonundaki hızı zamansız hız denkleminden;
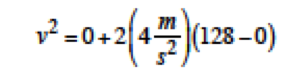
v=32 m/s olarak bulunur. Ayrıca aynı sonuç; v = v0 + at denklemi kullanılarak da aşağıda gösterildiği gibi elde edilebilir;
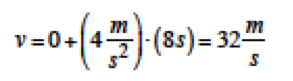
Şekilde durgun halden +x yönünde harekete başlayan bir araca ait hız (v)-zaman (t) grafiği görülmektedir.
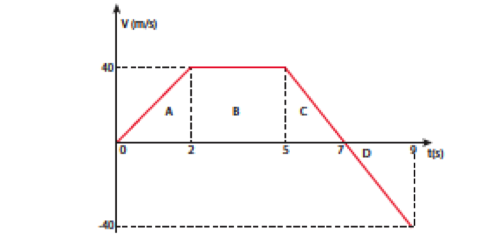
a) Aracın 2s sonunda aldığı yolu, b) Aracın (2-5)s arasında aldığı yolu, c) Aracın (0-2)s arasındaki ivmesini, d) Aracın (2-5)s arasındaki ivmesini, e) Aracın (7-9)s arasındaki ivmesini, f) Aracın (0-9)s aralığında aldığı toplam yolu ve toplam yer değiştirmesini bulunuz.
a) Hız-zaman grafiğinin zaman ekseni üzerinde ve grafiğin altında kalan alan pozitif yönde alınan yol miktarını verir. Bu durumda (0-2)s arasında bir dik üçgen mevcuttur. Bu alana A diyelim. Dik üçgenin alanı A’nın büyüklüğü;

olarak bulunur. Yani araç (0-2)s arasında 40 m yol almıştır. b) Aracın (2-5)s arasında aldığı yol hız-zaman grafiğinde bir dikdörtgene karşılık gelmektedir. Bu dikdörtgenin alanına B diyelim. Bu durumda;

olarak bulunur. Araç (2-5)s zaman aralığında 120m yol almıştır. c) Hız-zaman grafiğinde eğim ivmeyi verir, ayrıca genel olarak ivme denildiğinde ortalama ivme anlaşılmaktadır. (0-2)s arasındaki ortalama ivme a;
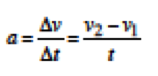
eşitliği ile verilir. Bu ifadede v2 aracın son hızı yani t=2 s anındaki hızı ve v1 ise ilk hızıdır. Grafikte görüldüğü üzere araç durgun halden harekete başladığı için ilk hızı yani v1=0’dır. t=2s anındaki hızı grafikten anlaşılacağı üzere 40 m/s’dir yani v2=40 m/s diyebiliriz. Bu durumda ivme;
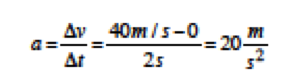
olarak bulunur. d) Araç (2-5)s arasında sabit hızla hareket etmiştir yani hızda değişim yoktur. Bu durumda, hareket bir boyutta olduğundan ivme sıfırdır. e) Aracın t=9s’deki hızı v2=-40m/s’dir. Eksi işareti aracın -x yönünde hareket ettiği anlamını taşır. Yine t=7s’deki hızı yani v1 sıfırdır. Bu durumda aracın ivmesi;

olarak bulunmaktadır. Bu sonuçta yer alan (–) işareti aracın negatif yönde (-x) hızlandığı anlamını ta- şımaktadır. f) Hız-zaman grafiğinin altında kalan alan, zaman ekseninin üzerindeyse +x yönünde alınan yolu, zaman ekseninin altındaysa -x yönünde kat edilen mesafeyi vermektedir. Bu durumda zaman eksenin üzerinde iki adet dik üçgen ve bir diktörtgen bulunmaktadır. Bunların alanlarına A, B ve C diyelim. Bu durumda;
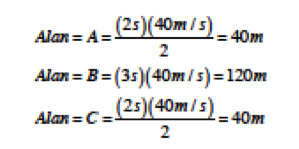
olarak bulunur. Bunun anlamı t=7s olana kadar aracın aldığı toplam yol A+B+C=40 m+120 m+40 m=200 m’dir. Zaman eksenin altında da bir dik üçgen vardır. Bunun alanına ise D diyelim. Bu durumda;
![]()
(–) işareti aracın -x yönünde hareket ettiği anlamını taşır. Şöyle diyebiliriz ki, t=7s olana kadar +x yönünde 200 m yol almış ve t=7 s ile t=9 s arasında –x yönünde yol almış yani araç başlangıç noktasına doğru yönelmiştir. Bu durumda aracın aldığı toplam yol 240 m olur. Fakat yer değiştirme 200 m - 40 m=160 m olur.