Introduction to Linear Programming
What is linear programming?
What is the "goal function"?
Goal function is the function that we try to maximize or minimize in an optimization problem.
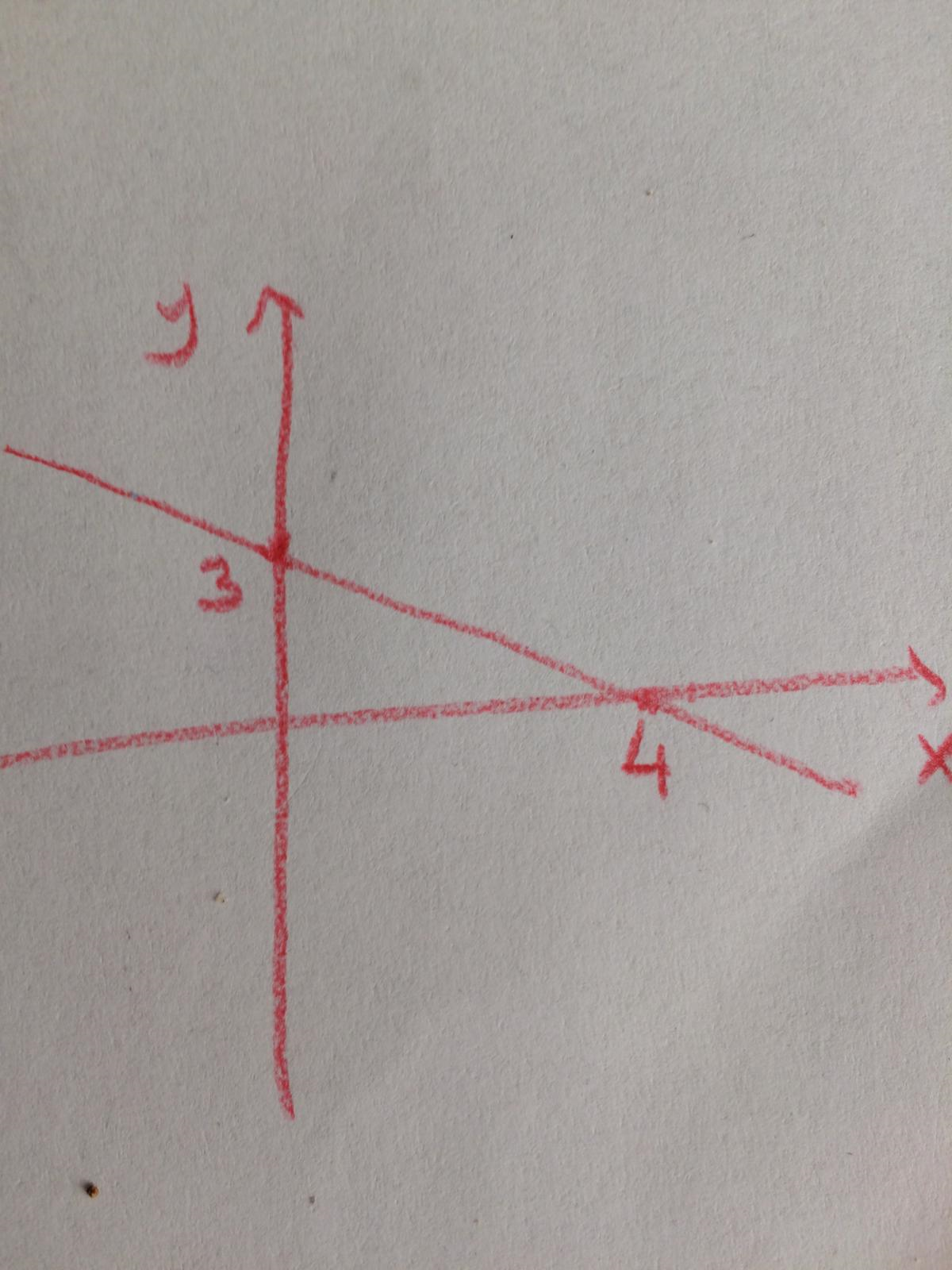
Draw the graph of the equation 3x+4y=12 on x-y plane.
In order to draw the graph of an equation we have to find the intercepts on x and y axis. To find the x-intercept we take y=0 and find x. Thus 3x=12, x=4 is the x-intercept. To find the y-intercept we take x=0 and find y. Thus 4y=12, y=3 is the y-intercept. So the graph is:
Define the solution set of a system of linear inequalities.
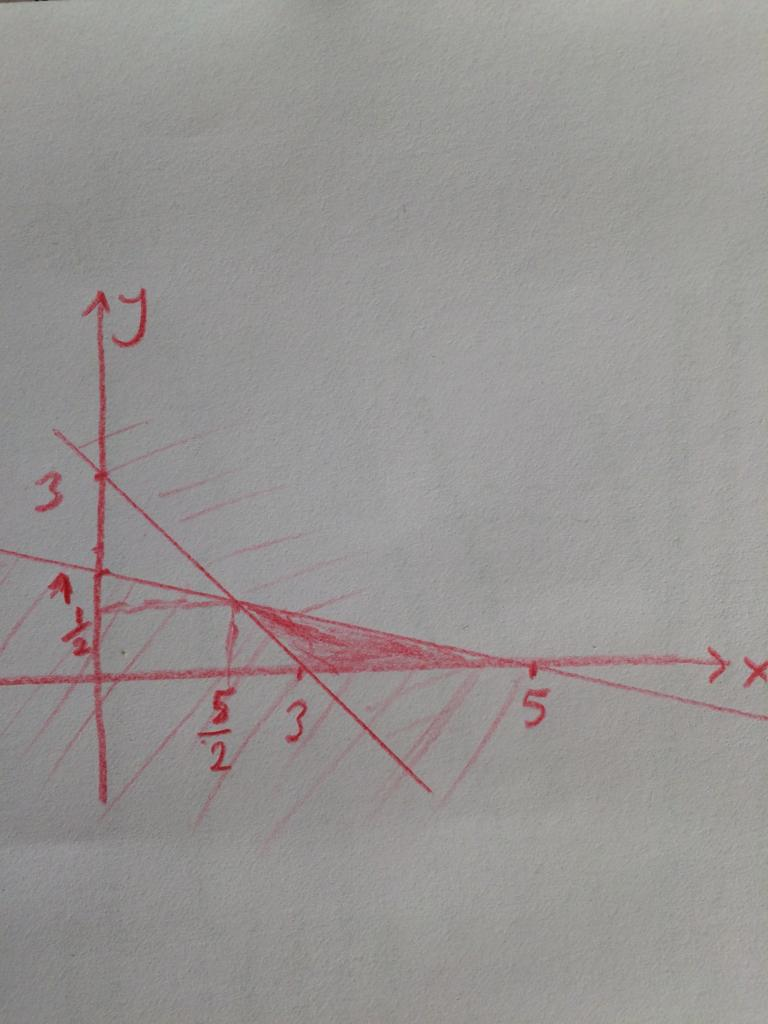
Draw the solution set of system of following linear inequalities:
x+y≥3
x+5y≤5
x≥0, y≥0
First we have to find the intercepts of the inequalities. For the first inequality:
x+y=3, x=3 when y=0 and y=3 when x=0
Since we have the "≥" expression we have to draw the right side of the line.
For the second inequality:
x+5y=5, x=5 for y=0 and y=1 for x=0
Since we have the "≤" expression we have o draw the left side of the line.
And since x≥0 and y≥0 we include only the non-negative values of x and y.
The last step is finding the intersection points.
x+y=3 so y=3-x
x+5y=5
by substituting y=3-x in the second equation we get:
x+5(3-x)=5, 15-4x=5, x=5/2 and y=3-x=3-5/2=1/2
Therefore intersection point is (1/2, 5/2)
Thus the solution set will be like:
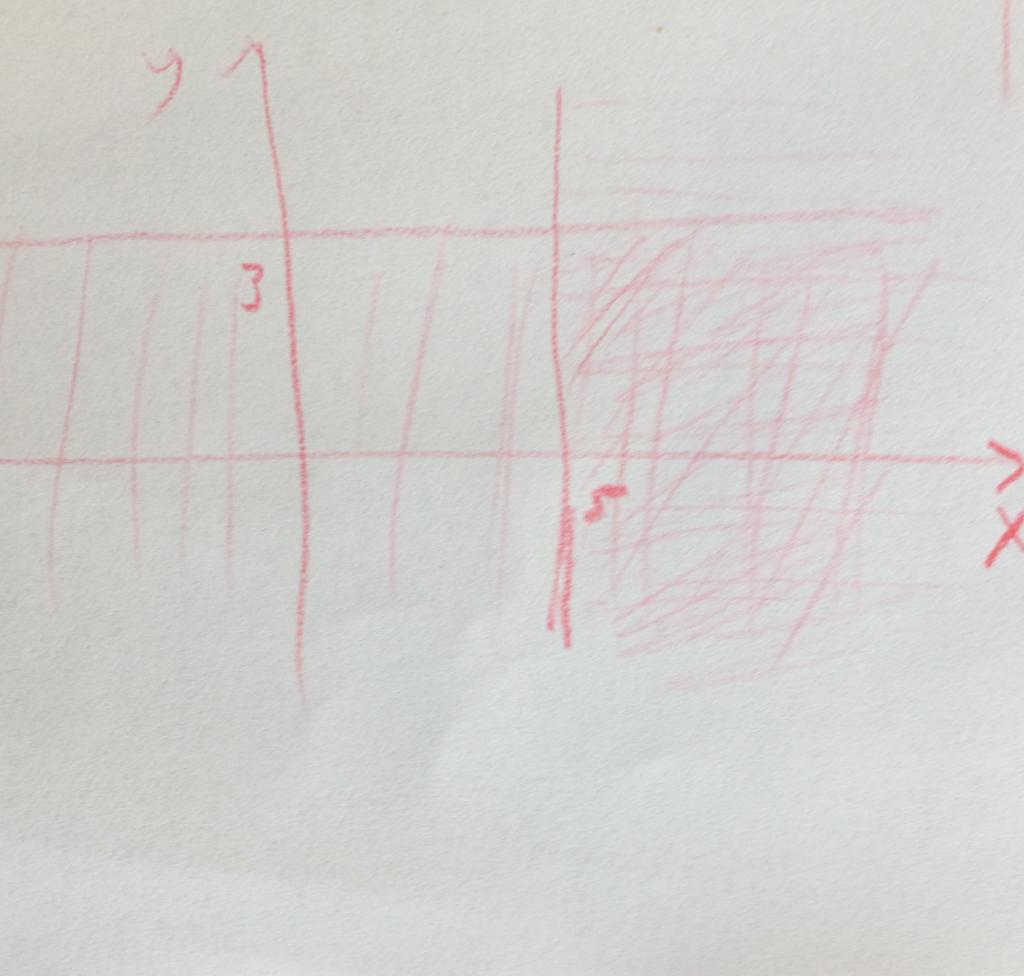
Find and draw an unbounded constraint set.
For example inequalities x≥5 and y≤3 results in an unbounded constraint set.
The graph of this set will be as:
Does the point (4,2) belong to the constraint set x+y≤5, y≤3, x≥0, y≥0?
The point (4,2) satisfies all other inequalities but it doesn't satisfy x+y≤5. Therefore it doesn't belong to the mentioned constraint set.
Show that the point (4,2) doesn't belong to the constraint set x+y≤5, y≤3, x≥0, y≥0 by drawing the solution set on the cartesian plane.
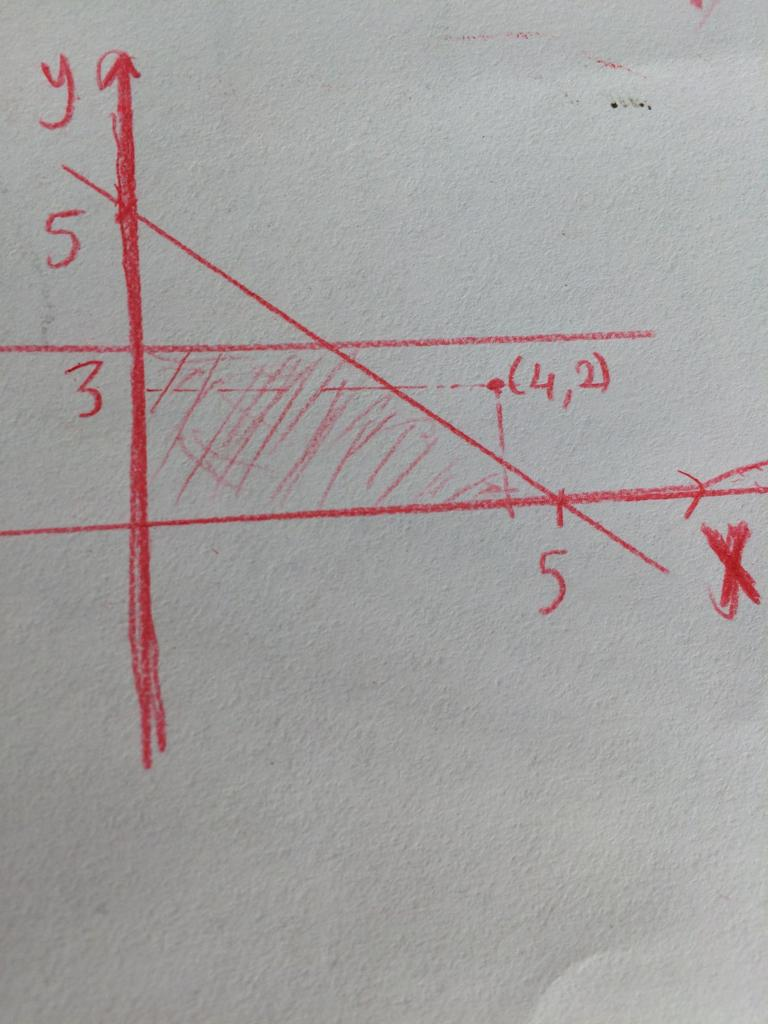
As shown in the drawing, the point (4,2) falls outside the shaded solution set.
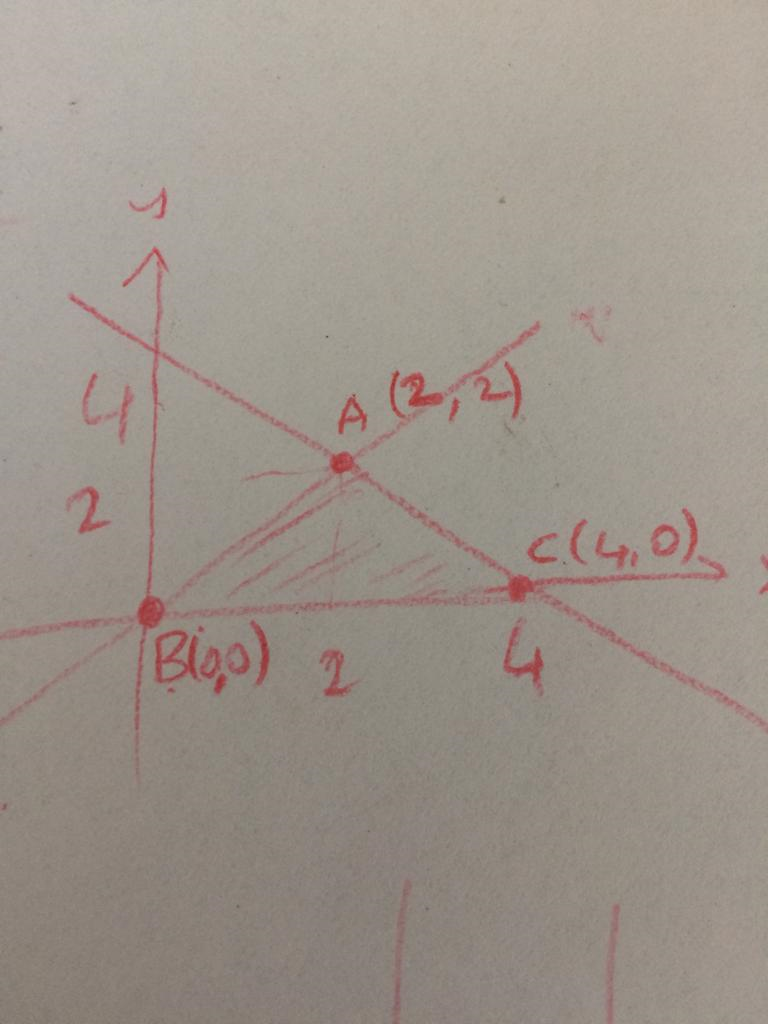
Find the corner points of the following constraint set.
x+y≤4
x≤y
0≤x, 0≤y
We find the corners by transforming the inequalities to equalities and solving the x, y values.
Thus instead of x≤y we take x=y, and instead of x+y≤4 we take x+y=4.
So x+y=2x=4, x=y=2. So point (2,2) is one corner (point A).
x=0 and y=0 is another corner point (point B). The x-intercept of equation x+y=4 is the third corner point which is (4,0), which is point C in the graph. So the graph will look like:
Define the Corner Point Theorem.
Corner point theorem states that the maximum or minimum of a linear function over the constrained set, if it exists, will necessarily occur at a corner point of the constraint set.
Find the maximum value of 4x+2y over the constraint set x≤y, x+y≤4, 0≤x, 0≤y.
Let's first find the corner points. If we substitute x=y in x+y=4 we get x=y=2. So one corner is point (2,2). Another corner is x=4, y=0. So the point (4,0) is the second corner. And the last corner is point (0,0).
For corner point (0,0), 4x+2y=0
For corner point (4,0), 4x+2y=16 *
For corner point (2,2), 4x+2y=12
Thus the maximum value of the goal function is 16.
Write the mathematical model of the following maximization problem. A factory produces product x and product y, whose prices are 5 and 10 respectively. The factory has 18 workers and 20 machines. 3 workers and 5 machines are used in production of each unit of x and 6 workers and 4 machines are used in production of each unit of y.
The goal function is 5x+10y subject to constrains
3x+6y≤18 (since 18 workers can be used at most, and since 3 workers are required per unit of x and 6 workers are required per unit of y)
5x+4y≤20 (since 20 machines can be used at most, and since 5 machines are required per unit of x and 4 machines are required per unit of y)
0≤x and 0≤y (since production quantities can not be negative).
Thus maximize 5x+10y subject to:
3x+6y≤18
5x+4y≤20
0≤x, 0≤y
Find the intersection point of the lines 5x-2y=18 and 2x+y=9
We can solve it by substitution. From the second equation we have y=9-2x. If we substitute y in the first equation we have:
5x-2(9-2x)=18
5x-18+4x=18
9x=36
x=4
Substituting this value in any of the equations we can find y.
So y=9-2x=9-2*4=1
Thus the intersection point is (4,1)
How are linear programming problems solved when the number of variables is two?
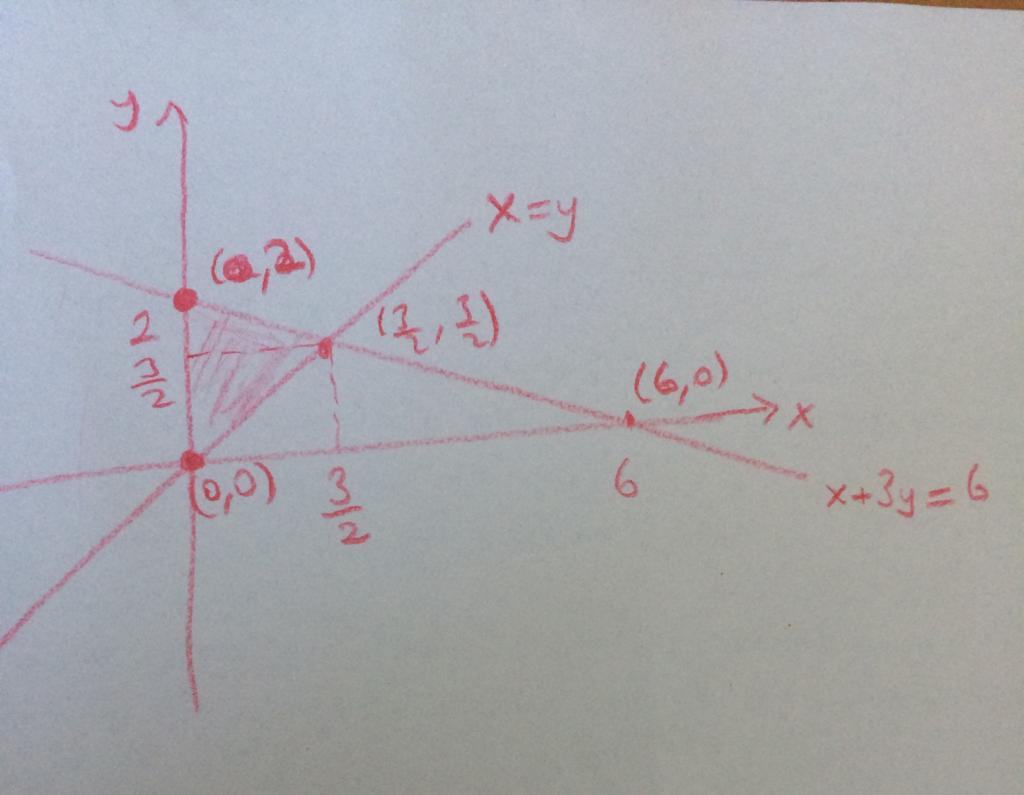
On cartesian plane show the corner points and solution set of the equation system:
x+3y≤6
x≤y
0≤x, 0≤y
We have to take inequalities as equalities to find the intersection points.
So we substitute x=y (from the second equation) in x+3y=6
Thus x+3x=6 then x=y=3/2. Thus the intersection point, and hence one corner is point(3/2, 3/2). Another corner is (0,0) and the last corner is the y-intercept of x+3y=6 line which is (0,2). So the graph looks like:
What is the maximum value of 3x+4y if 2x≤y, x+y≤6, 0≤x and 0≤y?
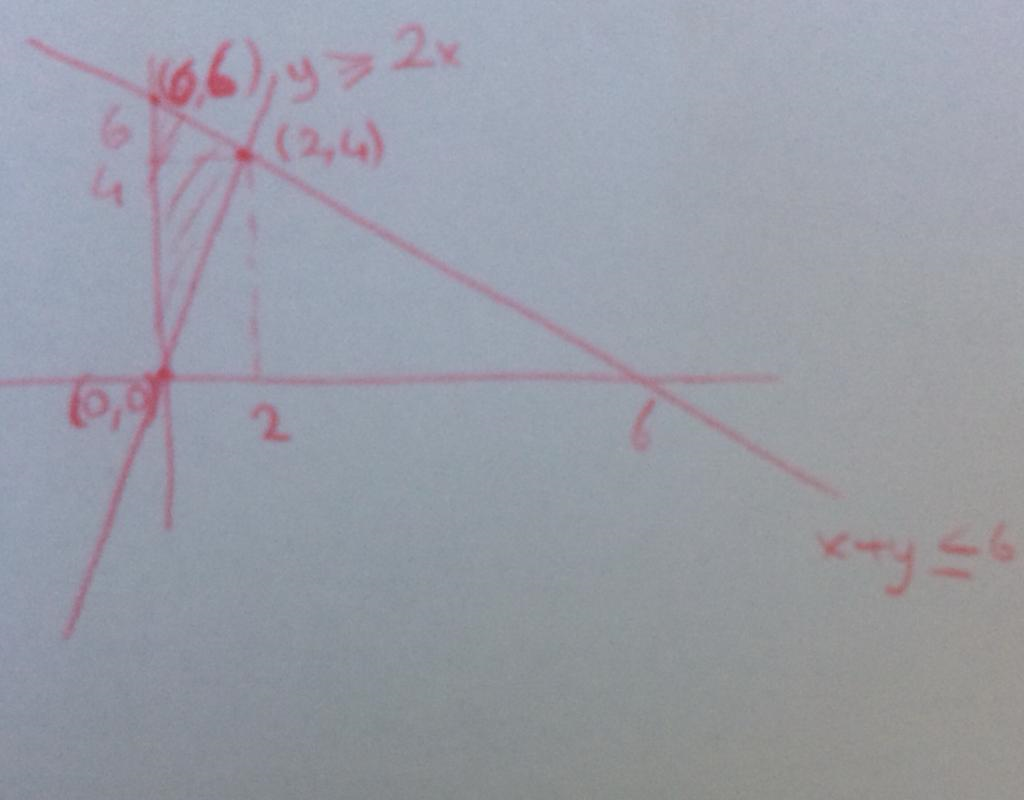
The corners of the solution set are (0,0), (0,6) and (2,4).
if we take corner (0,0) 3x+4y=0
if we take corner (0,6) 3x+4y=24
if we take corner (2,4) 3x+4y=22
Thus the maximum exists on the corner (0,6) which is 24.
Find the minimum value of f=3x+5y subject to constraints
x+y≥1
3x+2y≤6
0≤x, 0≤y
We have to first find the corners of solution set on the cartesian plane. For x+y≥1 the intercepts are x=1 and y=1, and the right side of the line should be shaded since it is a "greater than" sign. For 3x+2y≤6, the iintercepts are x=2 and y=3, and the left side of the line should be shaded since it is a "smaller than" sign.
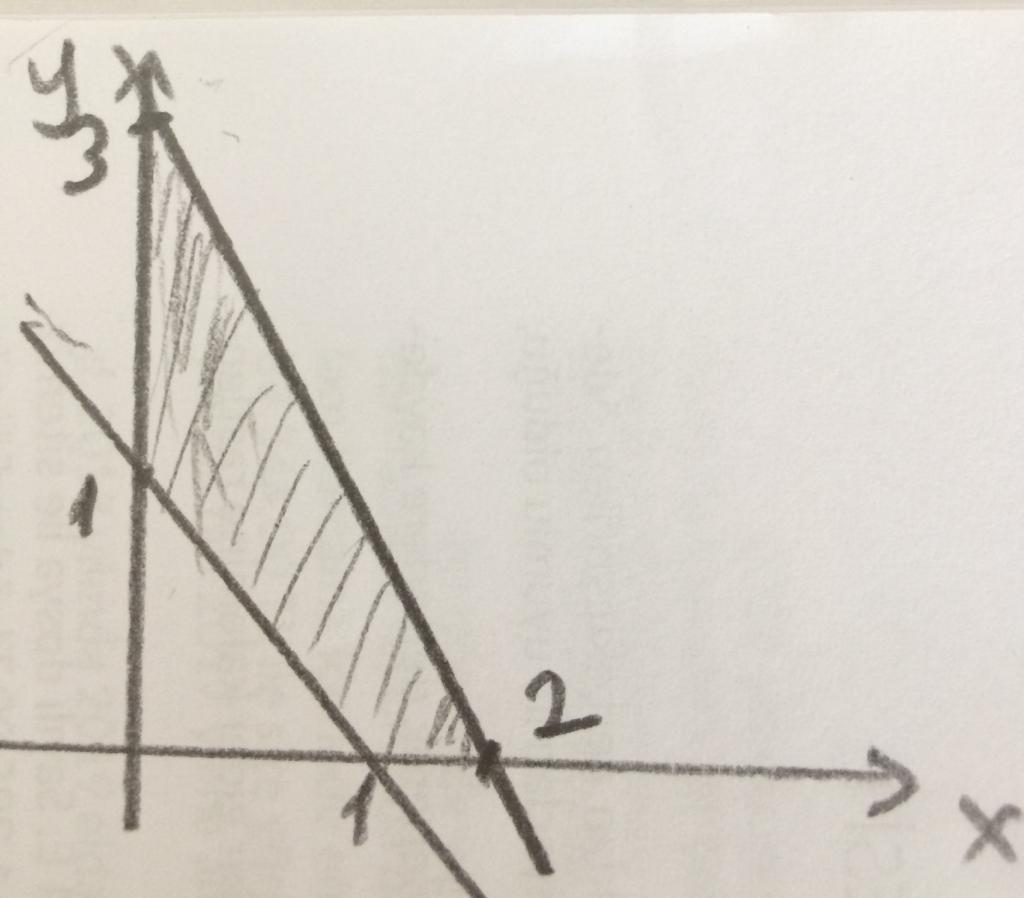
So the corners of the solution set are (0,1), (0,3), (1,0) and (2,0)
For (0,1), f=3x+5y=5
For (0,3), f=3x+5y=15
For (1,0), f=3x+5y=3 *
For (2,0), f=3x+5y=6
Thus the minimum value of f occurs at point (1,0) which is equal to 3.
Find the intersection point of the lines 3x+2y=17 and x-y=-1.
We can solve the system of equations by substitution. From the second equation we have x=y-1, and if we substitute this value of x in the first equation we have:
3(y-1)+2y=17
5y-3=17
y=4
From the first equation we have x=y-1=3.
Thus the intersection point (x,y) is (3,4).
Do the lines 3x+5y=8 and 6x+10y=9 intersect? If so, find the intersection point.
From the first equation we have y=(8-3x)/5. If we substitute the value of y in the second equation:
6x+10*((8-3x)/5)=9
6x+2*(8-3x)=9
6x+16-6x=9
16=9
Which is false. Therefore, the lines 3x+5y=8 and 6x+10y=9 never intersect, since they are parallel.
Find the intersection point of the lines 2x-y=9 and x+y=6.
From the second equation we have y=6-x. Substituting this is in the first equation we have:
2x-(6-x)=9
3x-6=9
3x=15, x=5, y=6-x=1
So the intersection point (x,y) is (5,1)