Matrices and Linear Equations
Define the square matrix.
If the number of rows and columns of a matrix are equal, then it is called a square matrix.
Define the rectangular matrix.
A matrix which is not square is called a rectangular matrix. Thus the number of rows and columns are not equal in a rectangular matrix.
What is an identity matrix?
The matrix of type n×n whose diagonal entries are 1 and the remaining entries are 0 is called the identity matrix of order n.
What is the condition for two matrices being equal?
Let A= [aij] and B= [bij] be matrices of order m×n. If aij=bij for all 1 ≤i≤m and 1≤j≤n (that is, the corresponding entries are equal), these two matrices are said to be equal.
What is the sum of the following two matrices
![]()
We just add all the components in the same row and column (i.e. a11+b11). So the sum will be:
![]()
Can we add a 3x2 matrix with a 2x2 matrix?
No. The number of columns and rows of two matrices should be same to do the addition operation.
If
![]() find 2A-B.
find 2A-B.
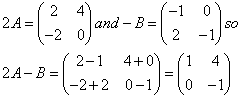
What is the condition for two matrices to be multiplied?
In order to be able to multiply two matrices, the number of columns of the first matrix must be equal to the number of rows of the second matrix. For instance we can multiply a 4x3 matrix with 3x2 matrix, and output will be a 4x2 matrix. However we can not multiply a 4x3 matrix with a 2x3 matrix.
What is an invertible matrix?
If a matrix A has an inverse, A is called invertible (or nonsingular); if such an inverse does not exist, A is called singular.
Find 3A if
![]()
We have to multiply all the components of the matrix with 3.
Thus:
![]()
Find AB, and BA if
![]()
Is AB=BA?
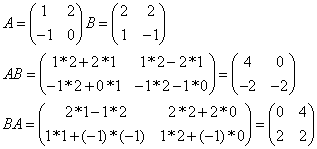
Thus AB is not equal to BA
What are the solution possibilities when we show a system of two equations on cartesian plane?
We obtain three possible cases for the solution of this system: 1. There is no solution if the lines are parallel. There is only one solution if the lines intersect. 3.There are infinitely many solutions if they coincide.
Find the determinant of matrix A if
![]()
detA=(1*0)-(2*-1)=0-(-2)=0+2=2
Is the following matrix singular?
![]()
The determinant of singular matrices is equal to zero. For the given matrix,
det(A)=1*6-2*3=6-6=0. So matrix A is singular.
Find the determinant of AB if
![]()
We dont have to multiply the matrices since det(AB)=det(A)*det(B).
det(A)=1*6-2*4=-2
det(B)=3*4-(-2)(-3)=12-6=6
So det(AB)=-2*6=-12
Write the following system of equations in matrix notation.
2x-5y=4
3x+2y=1
In order to write the equation system we have to first find the coefficient matrix. Then we write as CX=D where C is the coefficent matrix, X is the variable vector (x, y) and D is the right side of the equations.
Thus:
![]()
How many solutions does does the following equation system has?
x+2y=3
3x+6y=7
For an equation in the form ax+by=c, the slope of the line corresponding to the equation is -a/b and the x and y intercepts are c/a and c/b respectively. If the slopes of 2 lines are same and if they have different intercepts, then they are parallel, which in turn means the equation system has no solution. On the other hand, if the slopes and the intercepts are same then the lines coincide, which in turn means there are infinitely many solutions. Finally if the slopes are different then there is exactly one solution.
For the given equation system, slopes are same but intercepts are different. Thus they are parallel lines, which in turn means that the given equaion system has no solution.
Find det(A) if
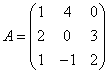
We will use Sarrus' rule:
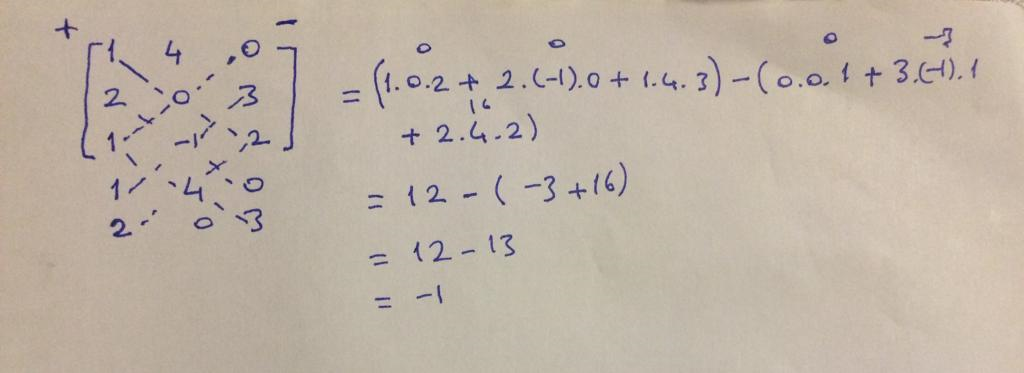
Find the inverse of the matrix A if
A=![]()
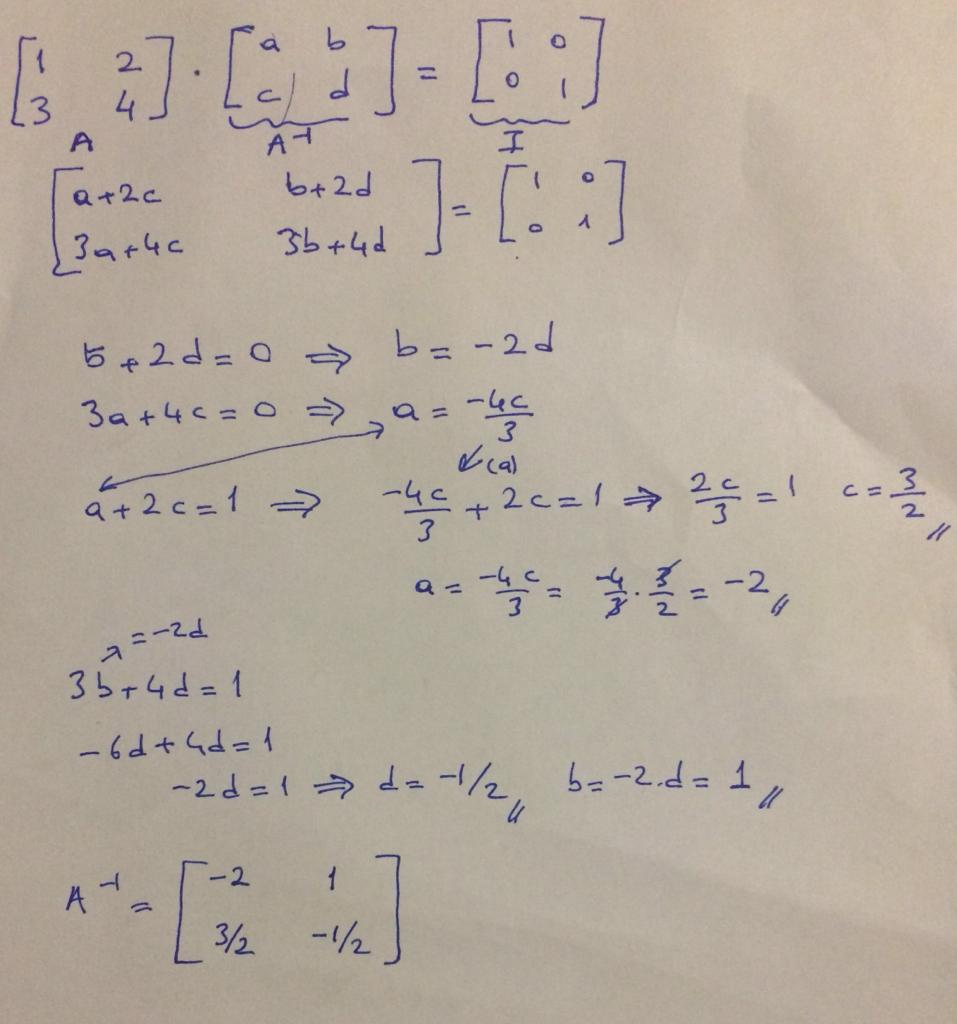
Find det(A+B) if
![]()
is det(A+B) equal to det(A)+det(B)?
![]()
det(A+B)=1 since it is the identity matrix.
However det(A)+det(B)=(-2-3)+(-2-3)=-10