aofsorular.com
MAT110U

Differential Equations

4. Ünite • 20 Soru
S

Define ordinary differential equations.

An ordinary differential equation (ODE) of the first order is an equation, containing the unknown function y=y(x), independent variable x, and the first derivative dy/dx.The general form of an ODE of the first order is F(x,y, dy/dx)=0

S

Find the general solution of dy/dx=2x+1

If dy/dx=2x+1 then y=x2+x+c (by integration)

S

Find the general solution of dy/dx=x2+2x-1

By integration y=1/3x3+x2-x+c

S

Find the function y(x) if dy/dx=2x and y(0)=-2

By integration y(x)=x2+c. So y(0)=c=-2. Thus y(x)=x2+c=x2-2

S

Find the general solution of the ODE dy/dx=2x/y

S

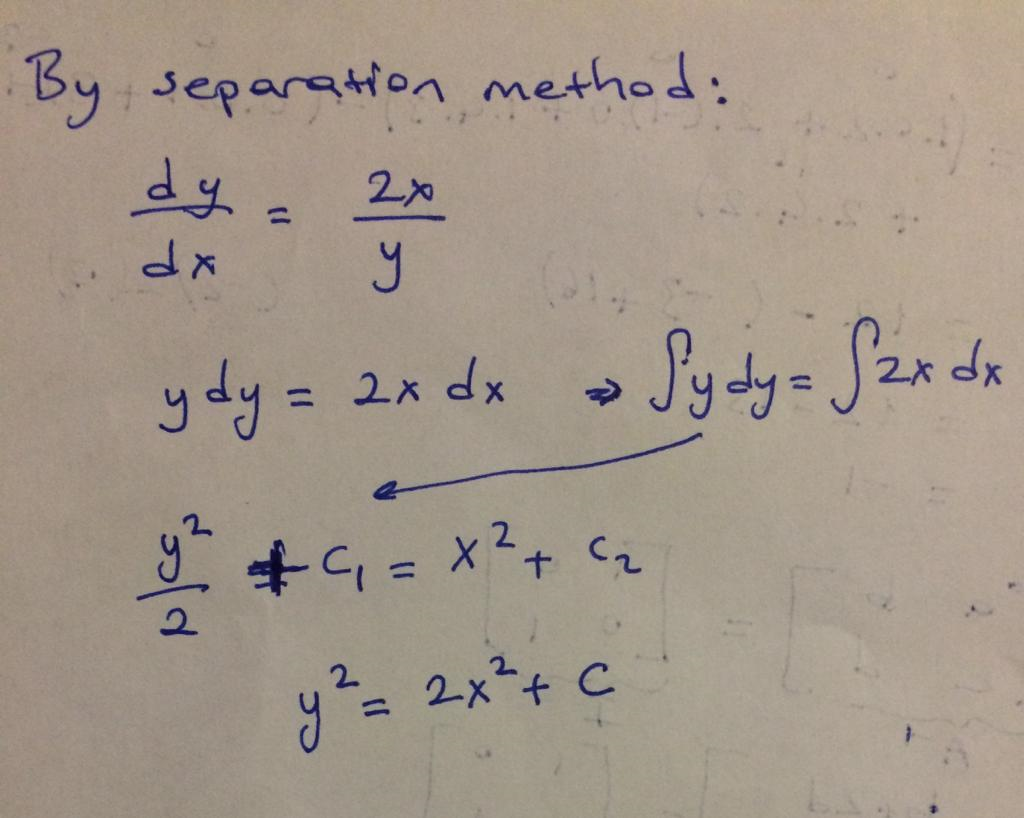
Find y(x) if dy/dx=(2x-1)/y and y(0)=3

S

Find y if dy/dx-2y=0

dy/dx=2y

by seperation method:

S

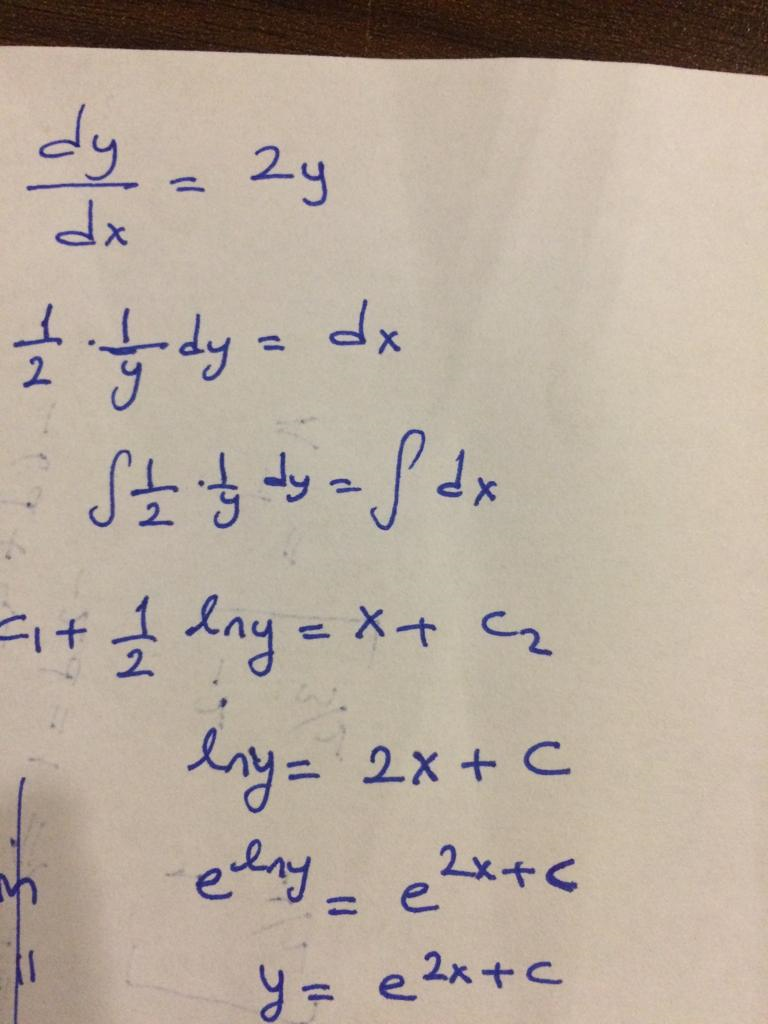
Find y(x) if dy/dx-xy=0

S

Find y(x) if dy/dx-4y=0

S

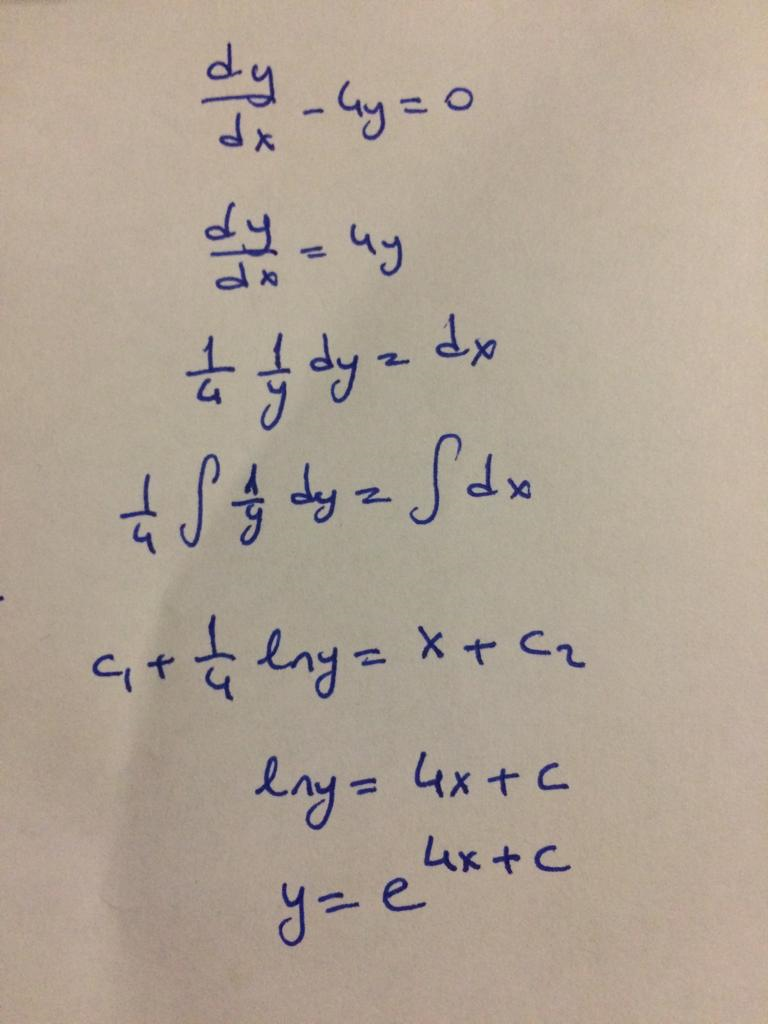
Find y(x) if dy/dx-2x/y=0 and y(0)=4

S

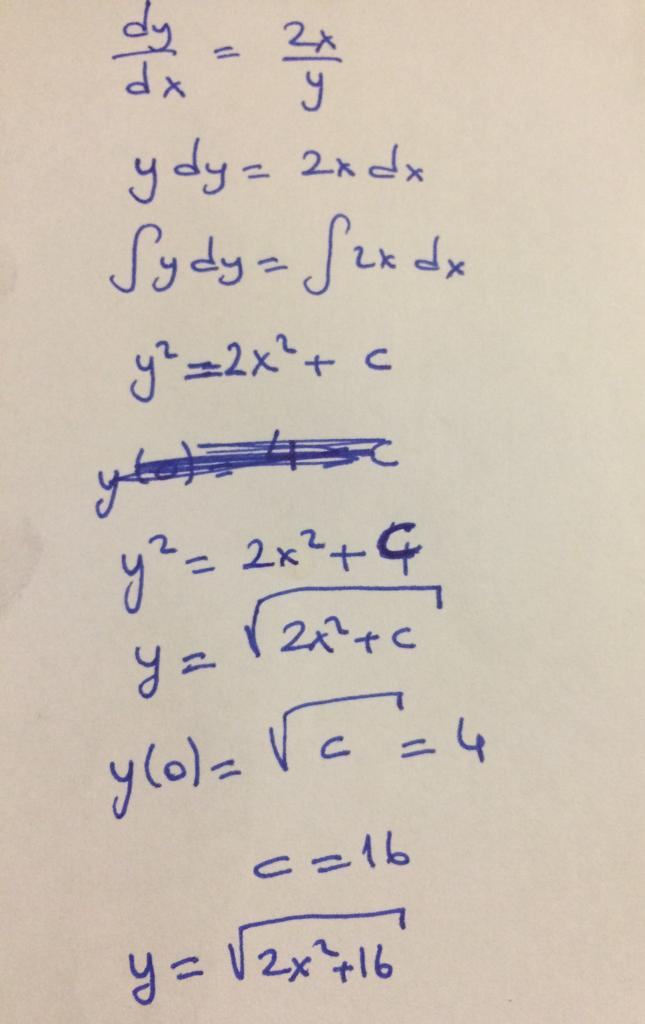
Find y(x) if dy/dx-1/x=0

S

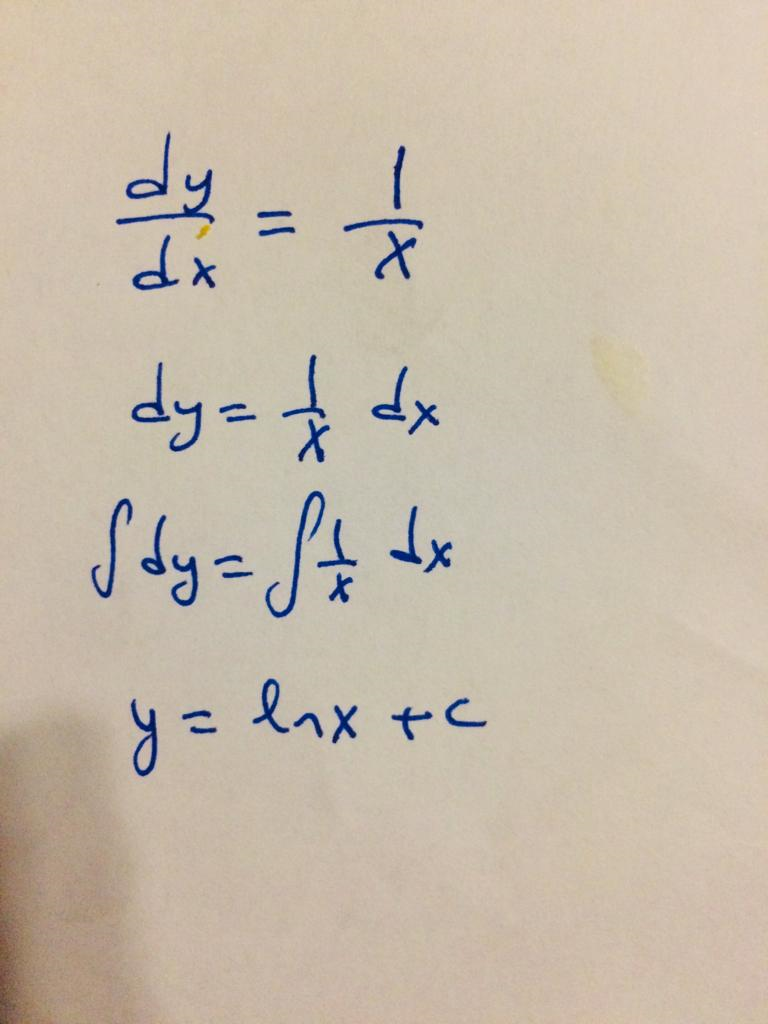
There were 100 rabbits in a cage at the beginning. In 8 months the population of rabbits increased to 200. How many months would it take for population to increase to 300?

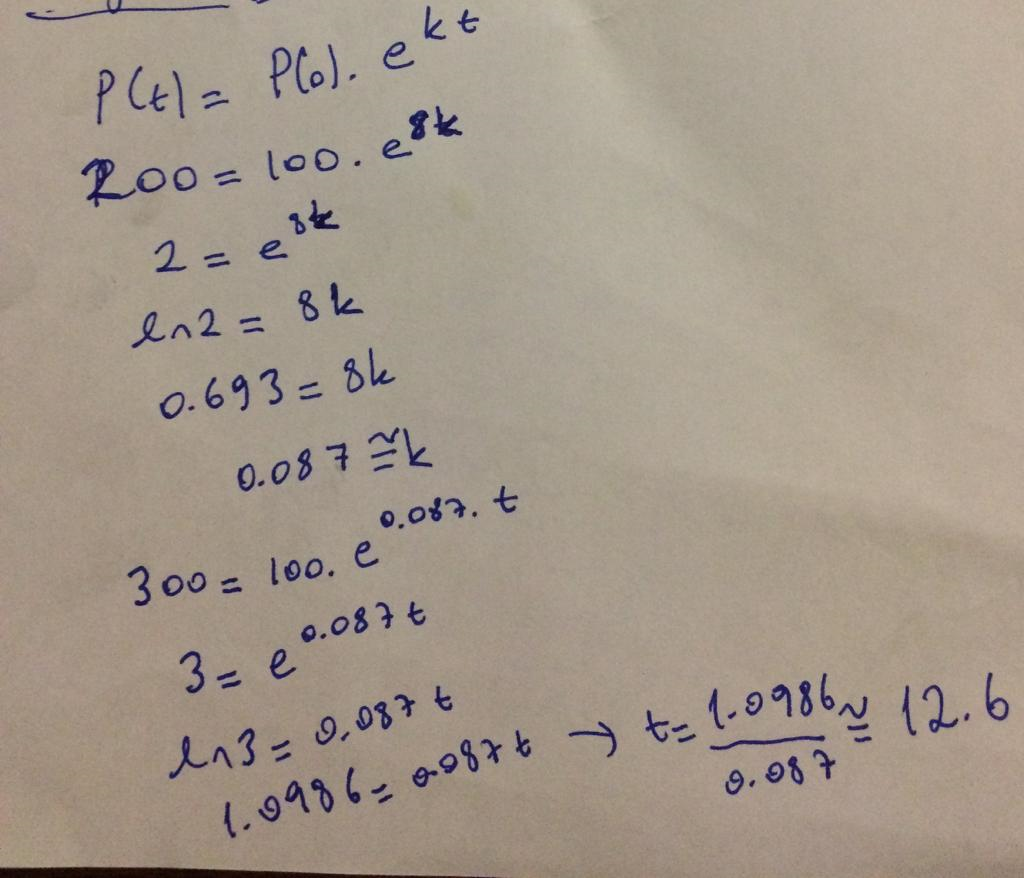
So the answer is 12.6 months.

S

A radioactive isotope has a half-life of 10 days. You wish to have 40 g at the end of 35 days. How much radioisotope should you start with?

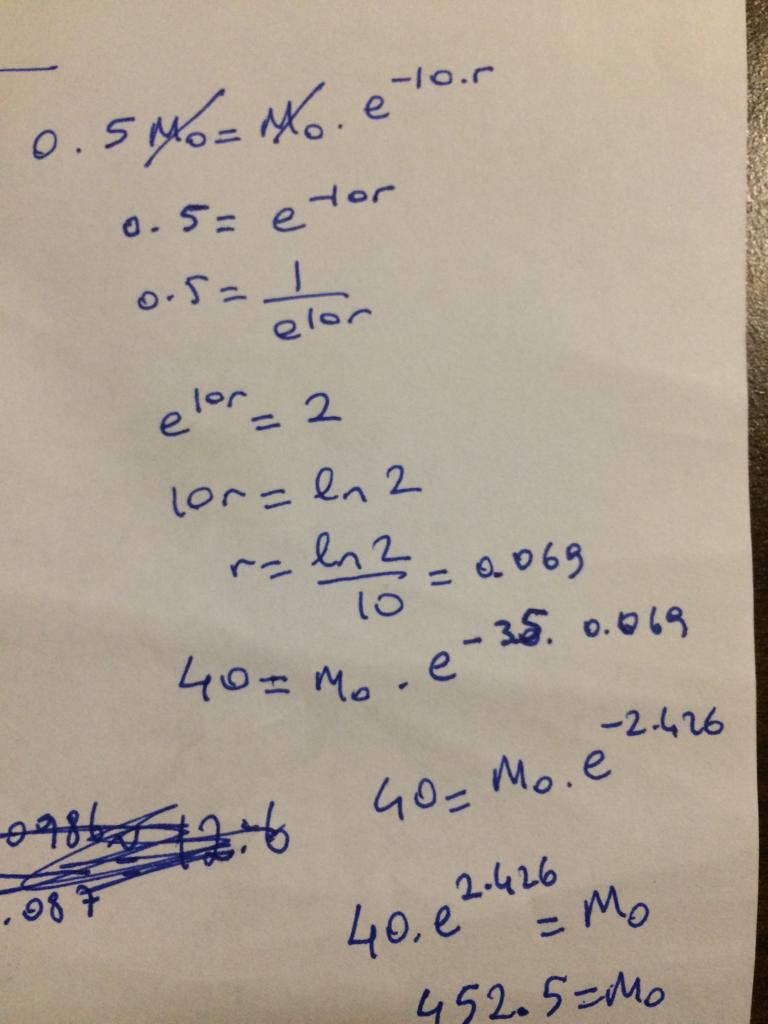
So the answer is 452.5 gr.

S

One can drink a coffee when its' temperature is at most 40 C. Assume that the temperature of the coffee cup was 70 C when it was put in to a can full of water whose temperature is 20 C. After 1 minute the temperature of coffee decreased to 60 C. In how much time the coffee will become drinkable? (its' temperature will decrease to 40?)

So the answer is 4.1 minutes.

S

Give an example where we can use logistic growth model of differential equations.

For example the number of the lions and antelopes would be a good example of logistic growth. When the number of antelopes is high, the population growth rate of the lions will be high. However, this in turn will cause a decrease in the number of antelopes, which causes back a decrease in the growth rate of lion population. Thus the growth rate of population of animals in restricted by the amount of food available.

S

Find the general solution for the following differantial equation

S

S

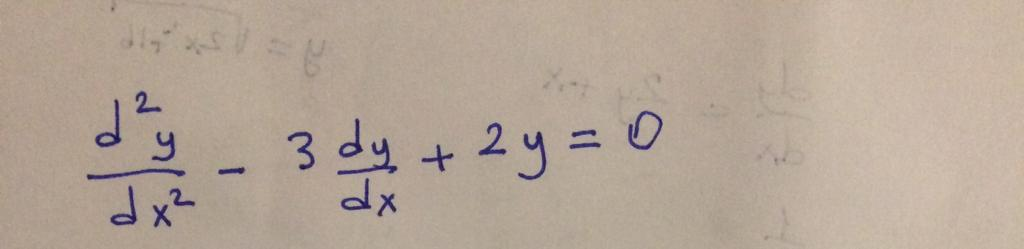
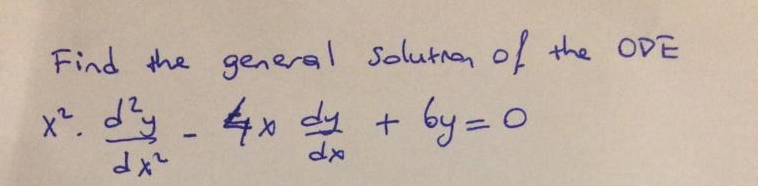
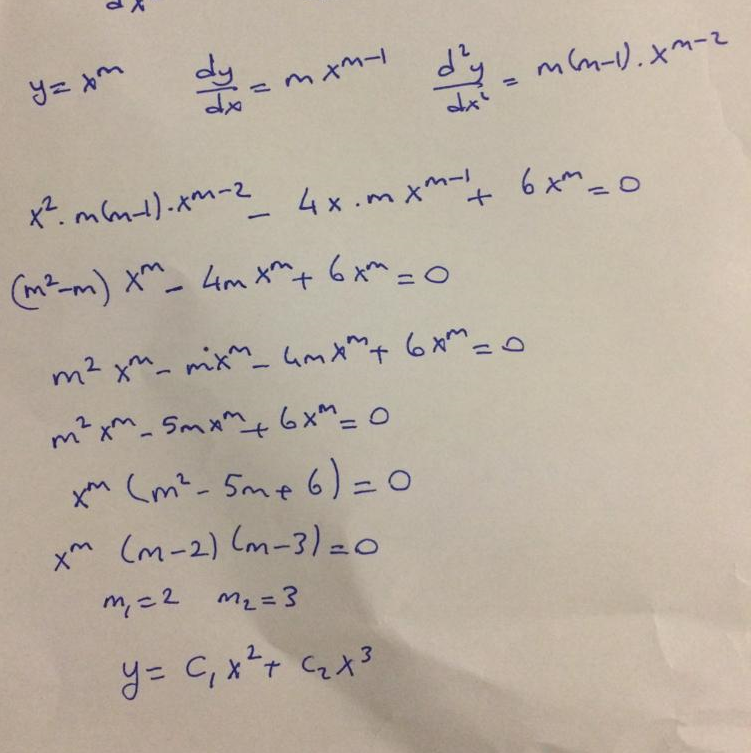
How can we solve a homogeneous linear ODE with constant coefficients?

A trial solution of the form y=emx should be substitute in the ODE, leading to a characteristic equation. If the ODE is of first order, then there is only one root m=m1, and the general solution is y=C1em1x. If the ODE is of second order, then there will be two roots m=m1 and m=m2 and the general solution is y=C1em1x+C2em2x

 
S

What are the main uses of differential equations?

Decay problems, compound interest, population inrease rate, heat problems, velocity and speed problems are most known uses.

S

What are the main types of the ordinary differential equations?

*DEs allowing separation of variables;

*linear ODEs;

*homogeneous linear ODEs with constant coefficients.