DOĞRUSAL PROGRAMLAMAYA GİRİŞ
eşitsizliğini sağlayan üç ayrı nokta yazınız.
eşitsizliğini sağlayacak x ve y değerleri olmalıdır. (x, y)={(1, 2), (5, 1), (1, 6)} değerleri verilen eşitsizliği sağlar.
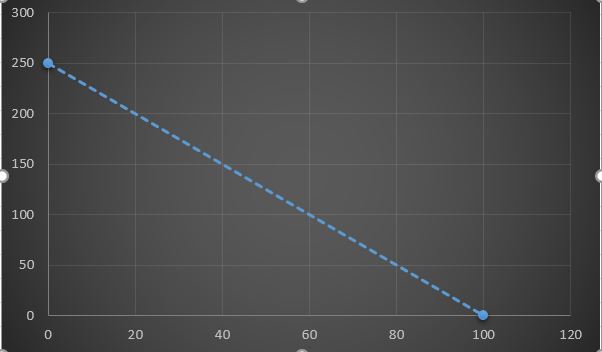
10x+25y<2500
eşitsizliğini sağlayan (x, y) ikililerini düzlemde göstererek şeklini çiziniz.
(x, y) noktasının bu eşitliği sağlaması demek, (x, y) noktasının bu doğru üzerinde olması demektir. Bir doğrunun grafiğini çizebilmek için, bu doğru üzerinde bulunan iki noktayı belirlememiz yeterlidir.
Önce 10x+25y=2500 denkleminde x=0 yazarsak; y=100 olup (0, 100) noktasını buluruz. Yine denklemde y=0 yazarak x=250 yani (250, 0) noktasını belirleriz. (0, 100) ve (250, 0) noktalarını birleştiren doğruyu çizerek 10x+25y=2500 eşitliğini sağlayan (x, y) noktalarını düzlemde işaretlemiş oluruz.
(4, 1), (1,3) ve (-3, 1) noktalarının 3x + 4y ≤ 9 eşitsizliğini sağlayıp sağlamadığını araştırınız.
(4, 1) noktası için eşitsizlik: 3*4+4*1≤9, 16≤9 eşitsizliği sağlanmaz.
(1, 3) noktası için; 3*1+4*3≤9, 15≤9 eşitsizliği sağlanmaz.
(-3, 1) noktası için; 3*(-3)+4*1≤9, -5≤9 eşitsizliği sağlanır.
(-2, 1), (5, -2) ve (1, 4) noktalarının 7x+4y>16 eşitsizliğini sağlayıp sağlamadığını araştırınız.
(-2, 1) noktası için; 7*(-2)+4*1>16, -10>16 eşitsizliği sağlanmaz.
(5, -2) noktası için; 7*5+4*(-2)>16, 27>16 eşitsizliği sağlanır.
(1, 4) noktası için; 7*1+4*4>16, 23>16 eşitsizliği sağlanır.
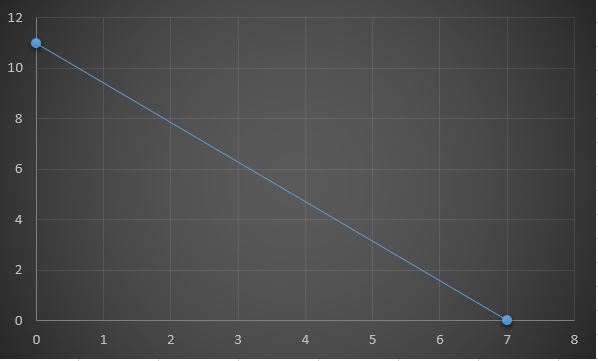
3x+y<15 eşitsizliğinin çözüm kümesini çiziniz.
3x+y=15 doğrusunun eksenleri kestiği noktalar:
x=0 için y=15 olup (0, 15) noktası ve y=0 için x=5 olup (5, 0) noktasıdır. (0, 0) noktası için 0<15 olup eşitsizliği sağlar.
(2, 1), (-1,3) ve (0, 1) noktalarının 2x+y<9 eşitsizliğini sağlayıp sağlamadığını araştırınız.
(2, 1) noktası için eşitsizlik: 2*2+1<9, 5<9 eşitsizliği sağlanır.
(-1, 3) noktası için; 2*(-1)+3<9, 1<9 eşitsizliği sağlanır.
(0, 1) noktası için; 2*0+1≤9, 1<9 eşitsizliği sağlanır.
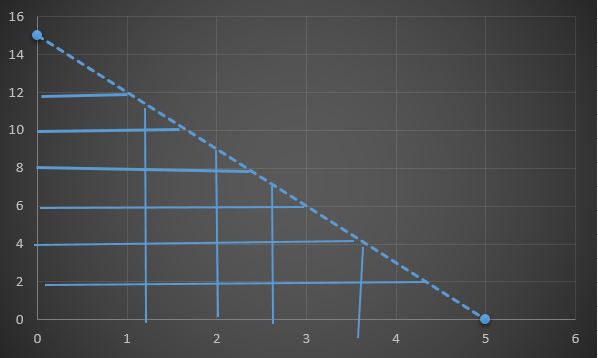
3x+y<9, x+3y<15, x>0, y>0 eşitsizliklerini sağlayan noktaların grafiğini çiziniz.
3x+y=9 için: x=0 için y=9 olup (0, 9) olur. y=0 için x=3 olup (3, 0) olur.
x+3y=15 için: x=0 için y=5 olup (0, 5) olur. y=0 için x=15 olup (15, 0) olur.
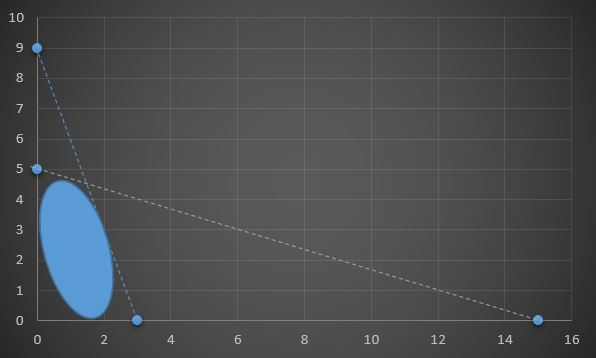
3x + 2y ≤ 6
x + y ≤ 5
x ≥ 0, y ≥ 0 eşitsizliklerini sağlayan noktaların grafiğini çiziniz.
3x+2y=6 için;
x=0 ise y=3 olup (0, 3) ve y=0 ise x=2 olup (2, 0)'dır.
x+y=5 için;
x=0 ise y=5 olup (0, 5) ve y=0 ise x=5 olup (5, 0)'dır.
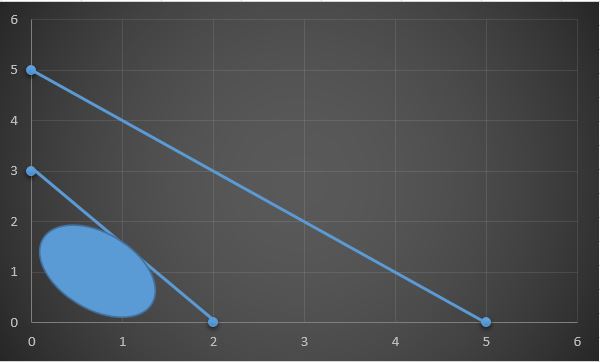
Her iki eşitsizliğin sağlandığı alan yuvarlak kesimle gösterilen kısımdır.
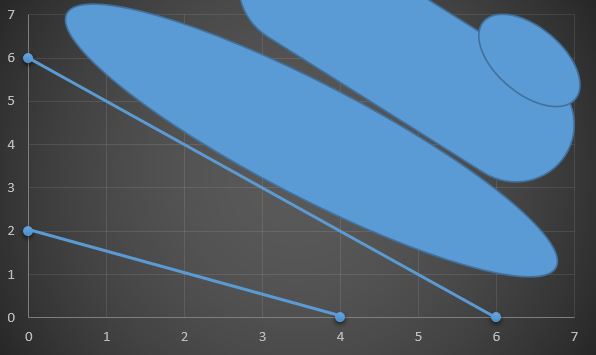
x + y ≥ 6
x + 2y ≥ 4
x ≥ 0, y ≥ 0 eşitsizliklerini sağlayan noktaların grafiğini çiziniz.
x+y=6 için;
x=0 ise y= 6 ve y=0 ise x=6'dır.
x+2y=4 için;
x=0 ise y=2 ve y=0 ise x=4 olur.
(4, 1), (1,3) ve (-3, 1) noktalarının x + 4y < 19 eşitsizliğini sağlayıp sağlamadığını araştırınız.
Verilen eşitsizliğin noktaları sağlayıp sağlamadığı kontrol edilirse;
(4, 1) noktası için; 4+4*1<19, 8<19 eşitsizlik sağlanır.
(1, 3) noktası için; 1+4*3<19, 13<19 eşitsizlik sağlanır.
(-3, 1) noktası için; -3+4*1<19, 1<19 eşitsizlik sağlanır
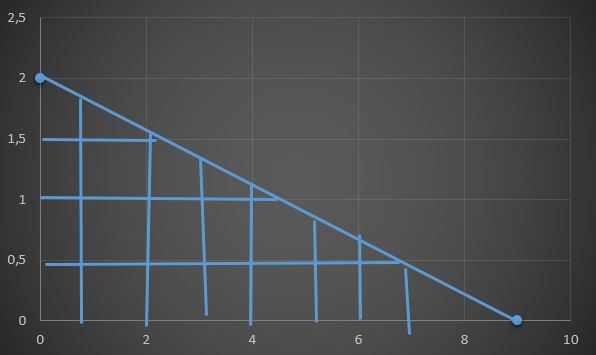
2x + 9y ≤ 18 eşitsizliğini sağlayan noktaların kümesini bulunuz.
2x + 9y = 18 doğrusunun eksenleri kestiği noktalar: x=0 için y=2, y=0 için x=9 olur.
Verilen eşitsizliğin grafiği;
0,3x+0,2y>12 eşitsizliğini sağlayan noktaların kümesini bulunuz.
0,3x+0,2y=12 denklemini sağlayan noktaları bulursak;
x=0 ise y=60 ve y=0 ise x=40 olup verilen eşitsizliğin grafiği:
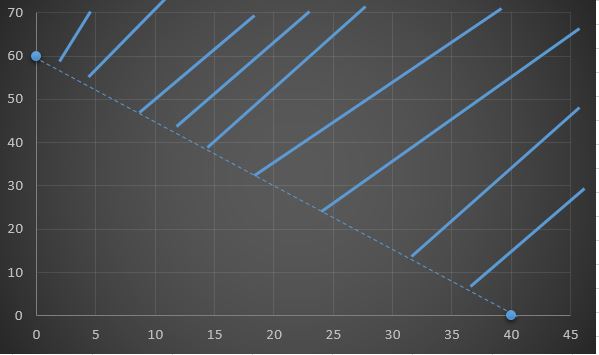
şeklindedir.
(x, y) noktasının bu eşitliği sağlaması demek, (x, y) noktasının grafik üzerindeki tüm noktaları sağlaması demektir. Bir doğrunun grafiğini çizebilmek için, bu doğru üzerinde bulunan iki noktayı belirlememiz yeterlidir.
x=0 için y=15 olur.
y=0 için x=2 olur.
(2, 0) ve (0, 15) noktalarını çizmek verilen denklem için grafiği belirlemede yeterlidir.
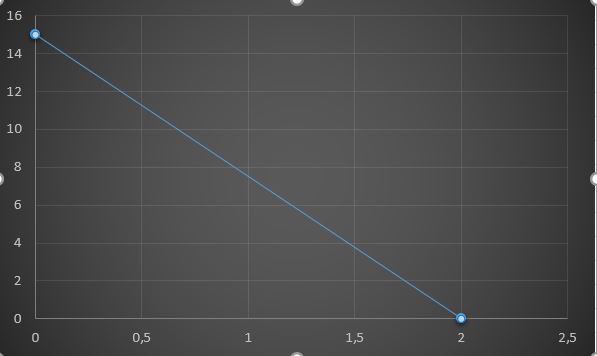
x=0 için y=5 olur.
y=0 için x=7 olur. (7, 0) ve (0,5)noktaları eşitsizliği sağlamaktadır.
Verilen eşitsizlik küçük olduğundan nokta nokta çizilen alt bölge sağlanır.
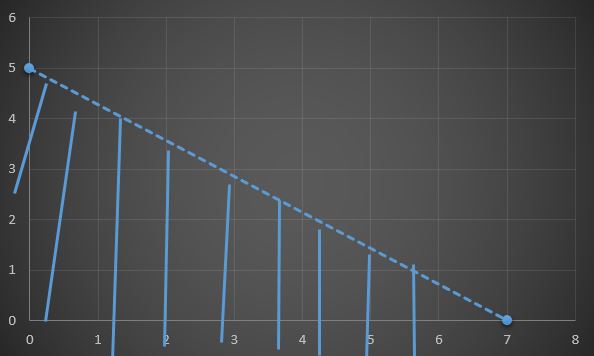
3x + y < 9
x + y < 5
x ≥ 0, y ≥ 0
eşitsizliklerini sağlayan noktaların grafiğini çiziniz.
3x + y < 9 eşitsizliği için 3x + y = 9 denklemi için noktaları bulursak; x=0 için y=9 ve y=0 için x=3 olur. (0, 9) ve (3, 0).
x + y < 5 eşitsizliği için x+y=5 denklemi için noktaları bulursak; x=0 için y=5 ve y=0 için x=5 olur. Bu iki denklemin grafiğini çizersek;
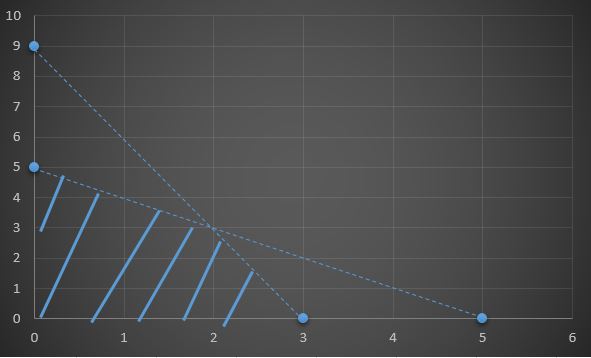
(2, 1), (1, 0) ve (-3, 1) noktalarının 2x + y ≤ 7 eşitsizliğini sağlayıp sağlamadığını araştırınız.
(2, 1) noktası 2*2+1=5≤7 olup (2, 1) noktası eşitsizliği sağlar.
(1, 0) noktası 2*1+0=2≤7 olup (1, 0) noktası eşitsizliği sağlar.
(-3, 1) noktası -3*2+1=-5≤7 olup (-3, 1) noktası eşitsizliği sağlar.
3x + y < 9
x + y < 5
x ≥ 0, y ≥ 0
eşitsizliklerini (2 ,1) noktası sağlamakta mıdır? Araştırınız.
(2, 1) noktasının eşitsizliklerinin sağlayıp sağlamadığını yerine koyarak araştırabiliriz.
3x+y<9 için (2, 1) noktasını test edersek; 3*2+1=7<9 olup eşitsizliği sağlamaktadır.
x+y<5 için (2, 1) noktasını test edersek; 2+1=3<5 olup eşitsizliği sağlamaktadır.
x + y ≥ 6
x + 2y ≥ 4
x ≥ 0, y ≥ 0 eşitsizliklerini (2, 5) noktasını sağlamakta mıdır? Araştırınız.
x + y ≥ 6 eşitsizliği için 2+5=7≥6 olup (2, 5) noktası eşitsizliği sağlamaktadır.
x + 2y ≥ 4 eşitsizliği için 2+2*5≥4 olup (2, 5) noktası eşitsizliği sağlamaktadır.
Verilen (2, 5) noktası iki eşitsizliği de sağlamaktadır.
(6 ,4), (2, 1), (3, 5) ve (7, 1) noktalarından hangilerinin 3x+4y<27 eşitsizliğini sağlayıp sağlamadığını araştırınız.
(6, 4) noktası; 3*6+4*4=32<27 olup eşitsizliği sağlamamaktadır.
(2, 1) noktası; 3*2+4*1=10<27 olup eşitsizliği sağlar.
(3, 5) noktası; 3*3+4*5=29<27 olup eşitsizliği sağlamamaktadır.
(7, 1) noktası; 3*7+4*1=25<27 olup eşitsizliği sağlar.
7x+11y=77 denkleminin sağladığı noktaların doğrusunu çiziniz.
x=0 için y=7 olup (0, 7) noktası denklemi sağlamaktadır.
y=0 için x=11 olup (11, 0) noktası denklemi sağlamaktadır.
