MATEMATİK I

f(x)=x³-x²+5x-12 if we put 5 instead of x then,

f(5)=5³-5²+25-12=125-25+25-12=113

f (x) = 7x - 3 and f ^–1(x)=(x+3)/7

(f ∘g)(1)=f(g(1)) hence g(1)=0 f(0)=5.(0)³=0

(gof)(x)=g(f(x)) then (gof)(7)=g(f(7)) by the way f(7)=1-7=-6 (gof)(7)=g(-6)=-6-2=-8

(f+g)(1)=f(1)+g(1)=1+3.1+1+12=17

(f.g)(3) =f(3).g(3)=3^-1.2.3-1=3^-1.5=5/3

for x=0 y=-2 then 2f(0)=2.-2=-4

From the graph we see that f(5/2)=-6 and f(-3)=8, so 2f (5/2)–f (-3)=(2.-6)-8=-20

Since f(x)=x²-1, let's find the image of each element of set A.

1²-1=0

2²-1=3

3²-1=8

4²-1=15

Thus, the image set is {0, 3, 8, 15}

The denominator for the functions in A, B, C and E equals to zero when x=1. Since a/0 is undefined 1 is not in the natural domain for these functions. Thus the answer is D, since f(x)=(x²-1)/(x²-x-2) is defined for x=1 (altough f(1)=0 !)

If f(a)=f(b) then a=b for one to one functions. Consider the function in A.

f(x)=x²-1

f(2)=3

f(-2)=3 but 2 is not equal to -2. Thus this function is not one-to-one. All the other given functions are linear and hence one-to-one. Note that f(x)=x³ is not linear but one-to-one also. Thus, all linear functions are one-to-one but not all one-to-one functions are linear.

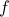 is onto (surjective)if every element of  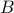is mapped to by some element of 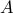. In other words, nothing is left out.

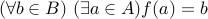Let all these functions defined from A to B (where both sets are set of natural numbers).It is clear that the function f(x)=x² is not onto because for instance 5 can not be square of a natural number. By the same logic the function in B is not onto since x² +5 can not be equal to for instance 4 if x is natural number. The functions in C and D are also not onto. Only f(x)=x is onto.

f(g(x)=(3x-1)²-1=(9x²-6x+1)-1=9x²-6x

suppose y=(3x-2)/4

We have to leave x alone on the right side and rewrite x as a function of y. 

So:

4y=3x-2

4y+2=3x

(4y+2)/3=x

Thus f^-1(x)=(4x+2)/3

since f(x)=x²+4, f(0)=4. Thus the graphs in A and B are eliminated. Also since x²+4 can not be equal to zero for real values of x, the graph can not cross the y-axis at y=0. Thus, E and D are eliminated also. Therefore the answer is C. Besides see that the coefficient of x² is positive. Therefore the function has a positive slope for x>0 and a negative slope for x<0.

f(g(x))=f(x²)=2+x². Thus for x=2, f(g(2))=6

Let's try to leave x alone from the expression f(x)=(2x-3)/(4x+1)=y

(2x-3)/(4x+1)=y

2x-3=y(4x+1)

2x-3=4xy+y

2x-4xy=y+3

x(2-4y)=y+3

x=(y+3)/(2-4y)

Thus f^-1(x)=(x+3)/(2-4x)

Since f(x)=3x-1 and g(x)=x²-1, then f/g(x)=(3x-1)/(x²-1).

For x=3, f/g(3)=8/8=1