Multivariable Functions
State the domain of the following function of two variables. Sketch the domains on the (x, y) coordinate frame.
State the domain of the following function of two variables. Sketch the domains on the (x, y) coordinate frame.
Evaluate the following limit.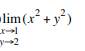
We start with substitution of the values, and in this case it turns out to be sufficient
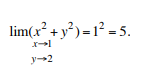
evaluate the following limit.
Here if we substitute x=y=0, we run into a problem, having 0/0 . Therefore, in order to resolve the singularity, we tend to the point (0,0) along a straight line of arbitrary slope, namely y=kx. Then, we have
Evaluate the following limit.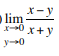
On substituting x=y=0, we have 0/0. Therefore we assume y=kx, which gives
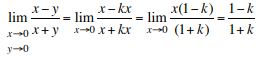
Thus, we have an answer depending on k. In other words, depending on the way we approach the point (0,0), the answer differs. That means that the limit does not exist.
Investigate the function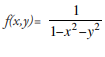
for continuity.
Clearly, the problems may appear only when the denominator is zero, i.e. x2+y2=1 which is a unit circle. It may also be observed, that as we consider the circle having the equation x2+y2=1+ε, where ε is a small positive number, then in the limit as ε tends to zero the function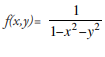tends to -∞. Similarly, if we consider the circle x2+y2=1-ε, so the function
and hence in the limit as ε tends to zero the function
tends to +∞. In fact, it may be shown that the graph of the function may be obtained by rotation of the graph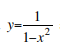
around the vertical axis.
For a function z=f (x, y) of two variables what first order partial derivatives do we have?
What are the rules for partial differentiation of a multivariable function?
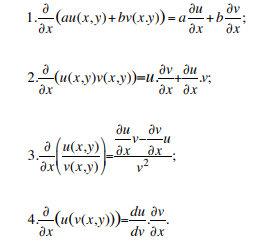
Calculate both partial derivative 
and 
of the following function.
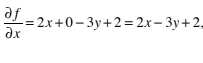
Calculate both partial derivative and of the following function.
Differentiating with respect to x means we need the product rule
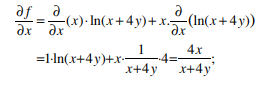
In contrast, since x is treated as a constant when differentiation is along y, we do not require product rule here
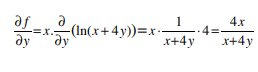
Note a multiple 4 arising due to chain rule.
Calculate both partial derivative and of the following function.
Applying quotient rule, we have
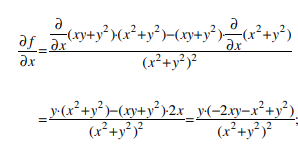
Similarly,
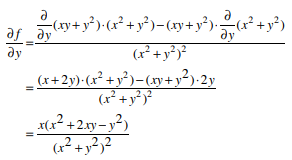
Calculate both partial derivative and of the following function.
Applying the chain rule, we get
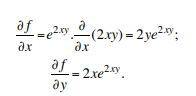
Calculate all of the second order partial derivatives for f (x, y) = x4 + y2 − 2xy and verify the Clairaut’s theorem.
First we find the first order derivatives
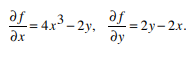
Then,
Thus, indeed 
and the Clairaut’s theorem is verified.
In analysis of functions of one variable, What is the differentiability of the function at a given point equivalent to?
In analysis of functions of one variable, the differentiability of the function at a given point is equivalent to having a finite derivative at this point.
For z = (x + y)-2, and x = u2+v2 and y=uv, find the partial derivatives
at u = v =1
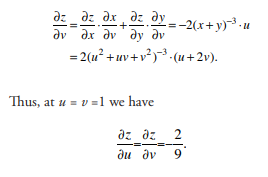
Find and classify the stationary points of the function f(x, y)=y2(x2+ y2-8)+8x2
A grocery store carries two brands of tomato juice, a local brand that it obtains at the cost of 3 TL per can and a well-known national brand that it obtains at the cost of 4 TL per can. The grocer estimates that if the local brand is sold for x TL per can and the national brand for y TL per can, approximately 7 - 5x + 4y cans of the local brand and 8 + 6x - 7y cans of the national brand will be sold each day. How should the grocer price each brand to maximize the profit from the sale of the juice.
Thus, and , so the obtained values x=5,3TL and y= 5,5 TL are the sought for prices maximizing the profit.
How would restricted local extrema of multivariable functions look like?
Below we consider in detail the case of a function of two variables. Then, there is usually just one restriction, so the formulation of the problem looks as follows
z=f(x, y)→extr
g(x,y) = 0
Here z = f (x, y) is often referred as the objective function, and g (x, y) = 0 is a constraint.
What is the simplest approach to the problem when there is restricted local extrema of multivariable functions?
The simplest approach to the problem is possible when one of the variables may be expressed in terms of the other from the constraint, then the problem reduces to standard extrema problem for a function of one variable.
A rectangular camping area of 2592 m2 needs to be designed. The area is bounded from one side by the forest and requires fencing from the other three parts (one length and two widths). Find the optimal length and width in order to have minimal length of the fencing required.
Let x and y be length and width of the designed camping area, respectively. Then the objective function, the fencing length is f (x, y) = x + 2y. The constraint of the area being 2592 m2 is written as xy = 2592, or xy -2592 = 0. Hence, then Lagrangian formulation is given by
Let us find the stationary points of this function. Then,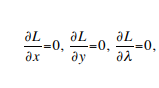
which gives
Eliminating λ from the first two equations, we have (clearly both x and y are not zero in view of the constraint)
hence x=2y, so from the constraint 2y2=2596, therefore y = 36, x =72, and the sought for length of the fence is 72+36+36= 144 m.