Applications of Derivative
What is demand?
In the simplest terms the definition of demand tells us the desire or willingness of a customer to pay a certain price for a particular item she wants to buy.
What is supply?
Supply is the amount of a product per unit of time that producers are willing to sell at various given prices when all other factors are held constant.
What does the Latin phrase ceteris paribus mean?
The Latin phrase ceteris paribus means “holding other things constant”. In economics it signifies the effect of one economic variable on another “keeping all other variables unchanged”
The mobile phone manufacturer BuyMe&UseMe predicts that the demand to their brand new smartphone will be 2000 units if its price is set to 1200 TL, and the demand will be 3000 units if the price is reduced 200 TL per item. Find the demand function for this new product.
As before, let x denote the demand and p the price of the product. We are given (x1, p1 ) =(2000,1200) and (x2, p2)=(3000,1000), since there is TL discount in the price. The demand line that passes through these points has slope m=-1/5 and its equation is p=-x/5 +1600 the graph of which is given below
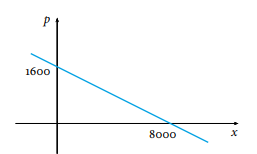
Our famous brand BuyMe&UseMe decides that they would make more money if they sell their new smartphone at a higher price even if the demand decreases slightly. They calculate that they may supply 1000 units at a price of 1100TL, or maybe with a slight increase in the price they may supply 1400 units at 1500TL. Find the company’s supply function.
The slope of supply line is
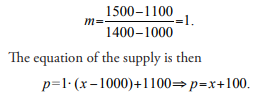
What is the equilibrium point?
The point where the quantity demanded equals the supply provided is called the equilibrium point.
What is the market price?
The price of a product at the intersection point, provided that it is in the first quadrant, is called market price.
What happend when the market is not in equilibrium?
When the market is not in equilibrium two cases appear: either there is shortage, this happens when supply is less than demand; or there is surplus, which takes place when supply is greater than demand.
What are fixed and variable costs?
The total cost of a production is composed of fixed costs such as buildings, rent, interest to be paid, and machinery costs, and variable costs which vary according to the quantity of a good produced and include inputs such as labour and raw materials. Even when there is no production the company still has to pay for the fixed costs.
What is the equation of the total cost?
If we denote the fixed cost by a, the number of units produced and sold by x, and the unit variable cost by ν, then the total cost function is written as
C (x) = νx + a.
What is the total revenue?
The total revenue function has a much straightforward definition: it is the product of the number of items sold, i.e. x, and the price per unit item which we denote by p. Therefore, we have
R (x) = px
What is the break-even point?
The break-even point is the point at which cost or expenses and revenue are equal: there is no net loss or gain, and one is said to have “broken even.
A hardware manufacturer company sells its new product for 130 TL per item. Total cost consists of a fixed cost of 4400 TL, and the production cost of 50 TL per item. What is the break-even point?
Let x denote the number of items produced and sold. The total revenue is R (x) = 130x
and the total cost is
C (x) = 50 x + 4400
where, now, ν=45.To find the break-even point we equate total cost to total revenue, so ![]()
so that x =55 Thus, the manufacturer has to sell at least 55 units to break even, i.e. no profit, or no loss.
What is the mariginal cost?
The additional cost needed to produce or purchase one more unit of a good or service is called the marginal cost. It corresponds to the derivative of the total cost function C(x).
What is the marginal revenue?
The extra revenue generated by selling one additional unit of a good or service is called the marginal revenue.
What is the marginal profit?
The derivative of the profit function P(x) is called the marginal profit and
P'(x)=R'(x)−C'(x)
The Kabachka company estimates that their new product, a fancy rucksack for ladies, will have a total cost of C(x)=x2/8+3x+98. The company demands that all x units of its product will be sold when the price is p(x)=(75-x)/3 TL per item. Determine the level of production that maximises the profit.
Since the demand function is p(x)=(75-x)/3 the total revenue function is
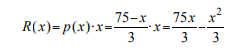
The total profit function is given by
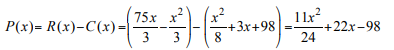
In order for the profit to be maximum, the derivative of the total profit, i.e. the marginal profit should be zero. Thus,
P'(x)= R'(x)−C'(x)=0, that is R'(x)=C'(x)
Let us now calculate the profit maximum. First, we find x that makes P ͵ (x)=0:
![]()
R''(24)=− 2, and C''(24)=1/ 4,
so R ''(24) < C ''(24), and consequently, the profit is maximum when x=24. Finally let us calculate the profit for x=24. Inserting this value in the profit function we find
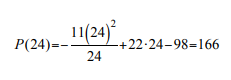
What is elasticity?
In economics, the term elasticity refers to the sensitivity (responsiveness) of one economic variable to changes in another economic variable. In order to prevent the use of dimensions, it is measured as the ratio of percentage changes, rather than absolute changes.
How can we interpret the price elasticity of demand?
We can interpret the price elasticity of demand as follows:
1. When Ep<1, the demand is inelastic (not elastic). We can say that the consumers are unresponsive (insensitive) to the changes in price: a change in price produces a smaller change in demand;
2. When Ep=1, the demand is unit elastic. The change in price results the same amount of change in demand;
3. When Ep>1, the demand is elastic. The consumers, in this case, are very sensitive to changes in price. Even a small change in price will probably result in a substantial change in demand.
What is the relationship between elasticity and revenue?
If demand is elastic, i.e. |Ep|>1, revenue R(p)=p q(p) decreases as price p increases.
If demand is inelastic, i.e. |Ep|<1, revenue R increases as price p increases. If demand is of unit elasticity, i.e. |Ep|=1, revenue is unaffected by a small change in price.