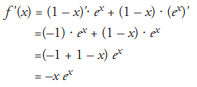Derivative and its Applications
What does the derivative of a function represent?
The derivative of a function represents the rate of change of a function at a particular point.
Find the slope of the tangent line to the curve y = x2 at the point (2, 4).
Denote the slope by m. Then
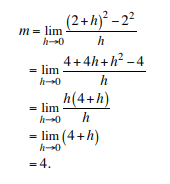
Find the slope of the tangent line to the curve y = x3 + 1 at the point (–1, 0).
Here f(x) = x3 + 1
f(–1) = (–1)3 + 1
= –1 +1
= 0
and
f(–1 + h) = (–1 + h)3 + 1.
The slope of the tangent at (–1, 0) is
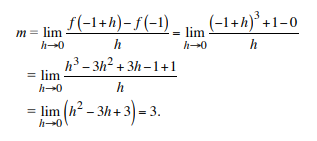
A particle moves along the x-axis in such a way that its position at time t is f(t) = 3t2+ t (metre). Find the average velocity vav over the interval [2, 4].
Here, t1=2 and t2=4. The values of f at these points are
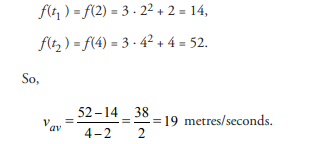
The motion of a particle is given by the function f(t) = t2 – 3t + 4. Find its velocity at the instant t = 2.
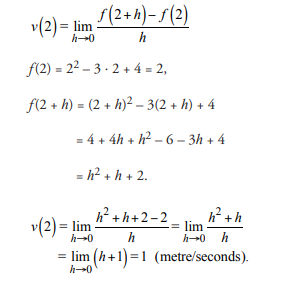
Given f(x) = x2, find the derivative f '(x).
We just need to apply the definition of derivative to the function f(x) = x2. On doing so, we get
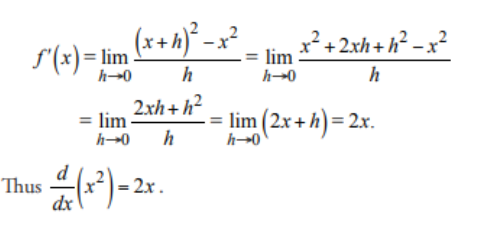
For a constant function f(x) = c, what is the value of the derivative?
For a constant function f(x) = c the derivative is zero, that is, (c)' = 0. Indeed,
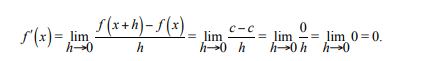
For the identity function f(x) = x, what is the derivative?
For the identity function f(x) = x, the derivative is 1, that is, (x)' = 1. Indeed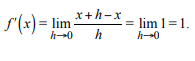
What is the derivative of a linear function f(x) = ax + b?
It can easily be shown that derivative of a linear function f(x) = ax + b is a, that is (ax+ b)' = a. For example,
(3x + 5)' = 3, (–2x – 2)' = –2.
What are the derivatives of some elementary functions?
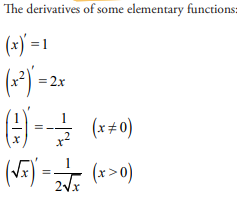
What is the power rule?
![]()
What are the derivatives of the exponential and natural logarithm functions?
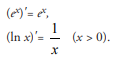
What is the product rule?
Let f(x) and g(x) be differentiable at x, then f(x) + g(x), f(x) – g(x), f(x) . g(x) and f(x) /g(x) (Here g(x) ≠ 0 must be satisfied) are also differentiable and
(f(x) + g(x))' = f' (x) + g'(x)
(f(x) – g(x))' = f ' (x) – g'(x)
(f(x) . g(x))' = f' (x) . g(x) + f(x) . g'(x)
(The Product Rule)
What is the quotient rule?
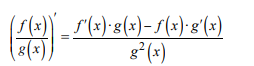
What is the constant rule?
From the product rule, it follows that if c ∈R is any constant, then
(c . f(x))' = c . f '(x) (The Constant Rule).
What is the chain rule?
The Chain Rule: The derivative of composite function f (g(x)) is f'(g(x)) . g' (x).
Find the second derivatives of the following functions at the point x = –1.
![]()
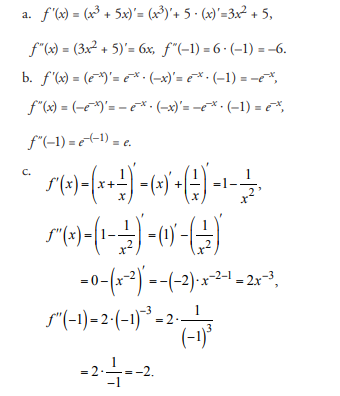
What is the equation of the tangent line to the curve y = f(x) at (x0, f(x0))?
The equation of the tangent line to the curve y = f(x) at (x0, f(x0)) is
y–f(x0)=f'(x0)(x–x0)
Find the local extreme point of f(x) = x2 – 2x.
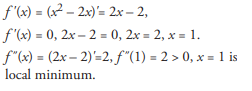
What are the local extremum points and intervals of decrease and increase of the function f(x) = (1 – x) ex?
The derivative of f is found by applying the chain rule as