Limits and Continuity
What is Calculus interested in ?
Calculus is interested in motion and change of quantities that depend on certain parameters through a rule. For example, the change of velocity of a car with respect to time, change in temperature with respect to the temperature of the surrounding environment, growth of a certain amount of money with respect to interest rate are only a few that comes to mind.
What are two fundamental concepts of Calculus?
It has two fundamentally significant concepts.The first of these concepts is the derivative, that is finding instantaneous change of a given function at a given point. It corresponds to the problem of finding the slope of a line tangent to a given curve at a given point on the curve. The second problem is concerned with finding the area of a plane region bounded by given curves. The solution of the problem of areas is the subject of the integral concept.
How is the average velocity of a moving object calculated?

Consider a car travelling 1,5 hours and covering a distance of 60 km and travelling for half an hour more to cover a total distance of 100 km. In this case how can the average velocity of the car during the time interval be calculated?
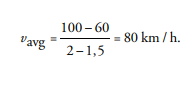
Suppose that a ball is dropped from the top of a tower of height 200m. What equation gives us the distance of the ball travels in the first t seconds?
Suppose that a ball is dropped from the top of a tower of height 200m. In the first t seconds, the distance of the ball travels is given by the equation
y (t)= 4,9t2.
Suppose that a ball is dropped from the top of a tower of height 200m. What is the average velocity of the falling ball from t=1 to t=2?
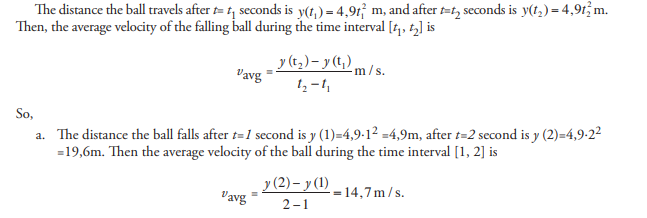
Suppose that a ball is dropped from the top of a tower of height 200m. How fast is the ball falling at the instant t=1?
Since we do not have any tools for finding the velocity of the ball at the instant t=1, it is not possible, at least for now, to find its velocity at the instant t=1. But we can calculate the average velocity over any time interval. So, we can first calculate the average velocity over a time interval [1, t] and let t get closer and closer to t=1. The distance the ball covers around time t=1 are calculated and presented in the following table.
![]()
Now, during short time intervals starting at t=1, we can evaluate the average velocities. These are given in the following table:
![]()
What equation gives us instantaneous velocity at the time t0?
If the function f (t) gives the distance of an object moving along the horizontal or vertical coordinate line then instantaneous velocity at the time t0
![]()
What is the tangent line problem?
The tangent line problem is the problem of finding a line that is tangent to a given curve (circle, graph of any function, etc.) at a given point P on the curve.
How do we read the following equation?
![]()
We read it as ‘’The limit of f as x approaches x0 is L ‘’.
What does ’x≠x0’ mean in the definition of limit?
Let us note that the expression ‘’x≠x0’’ in the definition of limit means that even though f may not be defined at the point x0, we can make the value of f (x) as close as we want to L.
What does the limit of a function at a given point x0 determine?
The limit of a function at a given point x0 determines the behaviour of the function near x0.
How does the fuction ![]() behave near x=2, that is lim x→2 f (x) = ?
behave near x=2, that is lim x→2 f (x) = ?
The domain of f is the set all real number except x =2 that is, the function f is not defined at x =2. The function can be simplified by cancelling the common factor (x - 2) of the numerator and denominator for x ≠ 2:
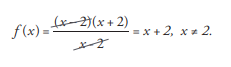
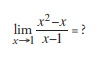
This question is an example of how an algebraic manipulation may be needed to calculate the limit at a given point. In the current case, the function is not defined at x=1 since division by zero is not allowed. However, the numerator of the function takes also the value zero at x =1, and it is not immediate how to calculate the limit. We generally encounter this situation in rational functions where both the numerator and the denominator takes on the value zero at the limit point, say x =x0. In our case, the function can be simplified by a factorisation in the form:
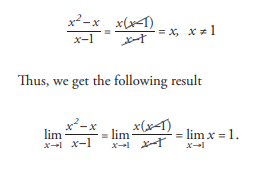
How are the right and the left limits of denoted?
![]()
It is read as the right limit of f is L.

Tt is said that the left limit of f is L.
What are the limit rules?
1. limit of a sum: 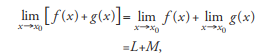
2. limit of a difference: 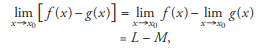
3. limit of a product: ![]()
4. limit of a constant multiple: 
5. limit of a quotient: 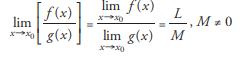
Find the value of the limit ![]() ?
?
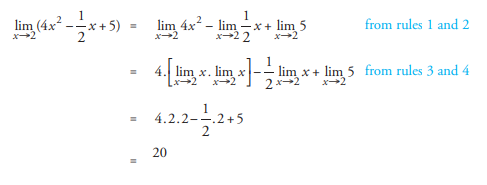
What do the symbols –∞ and +∞ represent ?
The symbols –∞ and +∞ do not represent numbers. They imply unbounded behaviour.
If f is continuous at the point x0, what three conditions must be ensured?
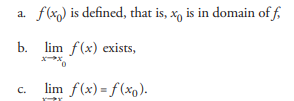
What do continuous on the interval and a continuous function mean?
If a function f is continuous at every point of the interval I, where it is defined, we say that f is continuous on the interval I. Also, if f is continuous at every point of its domain of definition, we say that f is a continuous function.