İstatistiksel Tahminleme
Tahminleme kavramı için istatistiksel bakışa göre bir tanım verebilir misiniz?
Günlük yaşamın hemen hemen her alanında parametre tahminlemesiyle karşılaştırılır. Bir araştırma sürecinin en önemli aşaması olan örneklemeyle tahminleme birbirinin ayrılmaz parçasıdır.
Tahminleme, tanımlanan evrenden seçilen rassal örneklemden hesaplanan istatistikler yardımıyla, bu evrenin uyduğu dağılımın parametre değerlerini araştırmaktır.
Tahmin ve tahminleyici nedir?
Hem örneklem hem de evren için bilgi üreten istatistiğe ilişkin formülasyona "tahminleyici", örneklem gözlem değerlerinin bir tahminleyiciye uygulanmasıyla hesaplanan değere ise “tahmin” adı verilir. Tahminleyici, tahminin nasıl hesap- lanacağını gösterir. Tahminse sayısal bir değerdir
Nokta tahminlemesini irdeleyiniz?
Tek bir rassal örneklemden hesaplanan θ istatistiğinin değerini, bu istatistiğin bilgi ürettiği θ parametresinin değerine eşit kabul eden tahminleme sürecine “nokta tahminlemesi” denir. Bu tahminleme bir atıcının hedefe tek bir atış yapması eylemine benzer. Tek bir atışın hedefteki gözlenen sonucuna bakarak, gözlenen sonuç tam isabet olsa bile atıcının iyi olduğunu söylemek doğru olmaz, tekrarlanan atışlardaki gözlenen sonuçlara bakmak gerekir. Bu benzetmeden hareketle nokta tahminlemesi tek bir örneklemden hesaplanan istatistiğin değerine dayanarak değil, bu istatistiğin örnekleme dağılımını inceleyerek yapılır.
Yansız tahminleyici nasıl tespit edilir?
Bir θˆ istatistiğinin örnekleme dağılımının beklenen değeri tahminlenecek evren
parametresine eşit ise θˆ istatistiği (tahminleyici) θ nın yansız tahminleyicisidir.
Yansız tahminleyicilerde önemli olan tahmin hatalarının cebirsel toplamının
dolayısıyla ortalamasının sıfıra eşit olmasıdır.
İstatistiksel tahminlemede etkinlik nedir?
Bir tahminleyicinin iyi bir tahminleyici olup olmadığını belirlerken kullanılan ikinci kriter tahminleyicinin etkinliğidir. Evren parametresine daha yakın örnekleme dağılımına sahip olan tahminleyici diğer tahminleyicilere göre daha etkin tahminleyicidir denir.
Bir yansız tahminleyicinin etkinliği; bu tahminleyicinin örnekleme dağılımının standart hatası (veya varyansı) ile ölçülür. Etkinlik, iki yansız tahminleyici arasında tercih yaparken kullanılan bir kriterdir. Eğer aynı örneklem hacmi esas alınarak hesaplanan iki tahminleyici yansız tahminleyiciler ise bunlardan standart hatası küçük olan, diğerine göre daha etkin tahminleyicidir. Bazı durumlarda az miktarda yanlılığa sahip, standart hatası küçük olan tahminleyici yansız fakat standart hata- sı büyük bir tahminleyiciye tercih edilebilir.
Tek evren parametresine ilişkin nokta tahminlemesini açıklayınız?
Tek evren parametresine ilişkin nokta tahminleme sürecinde aşağıdaki aşamalar izlenir:
Tanımlanan evrenden, belirlenen n birimlik (hacimli) bir basit rassal örneklem seçilir. Bu örneklemdeki birimler üzerinden ilgilenilen değişken itibarıyla veriler derlenir. Bu veriler kullanılarak tahminlenecek parametre θ için bilgi üretecek θˆ istatistiği hesaplanır. Son olarak bu istatistiğin değerinden ve dağılımının özelliklerinden yararlanarak θ parametresi için tahminleme yapılır.
Evren aritmetik ortalaması nokta tahminlemesi nasıl yapılır?
Bilindi¤i gibi μ için bilgi üreten istatistik, tahminleyici dır. Tanımlanan evrenden basit rassal örneklemeyle n hacimli bir örneklem oluşturulur ve (
) hesaplanır ise hesaplanan
birinci ünitede açıklandığı gibi bir rassal değişkendir.
nın beklenen değeri E (
) daima evren ortalaması μ ye eşittir ve onun yansız tahminidir.
Bu bilgiye göre μ nün nokta tahminlemesi,
şeklinde yazılır.
Tanımlanan pek çok evrenin ortalama bilgisi için genellikle örneklem aritmetik ortalaması en küçük varyansa sahip ve daima yansız tahminleyici olduğundan diğer ortalama (medyan gibi) tahminleyicilerine tercih edilen bir tahminleyicidir.
Evren oranının nokta tahminlemesi nasıl oluşturulur?
Örnekleme uygulamalarının pek çoğunda evren oranı hakkında bilgi elde edilme- si istenir. Bu durumda π için bilgi üreten istatistik örneklem oranı p olur.
Evren oranı π ye ilişkin nokta tahminlemesi bir rassal örnekleme planında oluşturulan n hacimli bir örneklem için r bir binom rassal değişkeni olmak üzere, hesaplanan p=r/n oranının değerini π ye eşit aln bir tahminleme sürecidir.
Buradan p ’yi π nin yansız ve küçük varyanslı nokta tahminlemesi
şeklinde yazılır
İki evren ortalaması arasındaki fark için nokta tahminlemesi yapılır mı? Açıklayınız?
Tanımlanan iki evrenden, belirlenen n1 ve n2 birimlik (hacimli) basit rassal örneklemler seçilir.
Bu örneklemlerdeki birimler üzerinden ilgilenilen değişken itibarıyla veriler derlenir.
Bu veriler kullanılarak tahminlenecek parametre (θ1 - θ2) için bilgi üretecek θˆ1 - θˆ2 istatistiği hesaplanır.
Son olarak bu istatistiğin değerinden ve dağılımının özelliklerinden yararlanarak ilgili parametre için tahminleme yapılır.
İki evren oranı arasındaki farkın nokta tahminlemesi nasıl yürütülür?
İki evren oranı (iki binom parametresi) arasındaki farkın nokta tahminlemesi, iki evren ortalaması arasındaki farkın nokta tahminlemesine benzer.
Birbirinden bağımsız n1 ≥ 30, n2 ≥ 30 birimlik rassal örneklemler seçilirse bu örneklemlerden hesaplanan p1 ve p2 örneklem oranları arasındaki farkı gösteren (p1 - p2) istatistiğinin örnekleme dağılımının ortalaması iki evren oranı arasındaki fark parametresine eşittir ve yansız nokta tahminidir. Bu bilgiye göre parametresinin nokta tahmini
şeklinde yazılır.
Aralık tahminlemesi nedir?
Aralık tahminleme süreci hakkında bilgi verebilir misiniz?
Bir tahminleme sürecinde, küçük varyansa (ya da standart hataya) sahip olan tahminleyicinin tercih edilmesi, önemli bir kriterdir. Standa
Aralık tahminlemesi genel gösterimi nedir?
Bir parametrenin örneklem istatistiğine dayanarak örneklemenin planlama aşamasında araştırmacı tarafından belirlenen bir olasılığa (güven düzeyine) göre simetrik bir aralıkta belirlenmesi çalışmasına aralık tahminlemesi denir.
Bu tanıma göre θ parametresinin aralık tahminlemesinin gösterimi genel olarak
A < θ< Ü
şeklinde yazılır. Burada A ve Ü tahminlenecek parametre değerini kapsayacak alanı belirleyen sınır değerleridir. Güven sınırları adı verilen bu sınırlardan A, alt sınır; Ü, üst sınır olarak tanımlanır.
Evren ortalamasının mümkün örneklemlerdeki aralık tahminlerinin dağılımı grafiğini oluşturunuz?
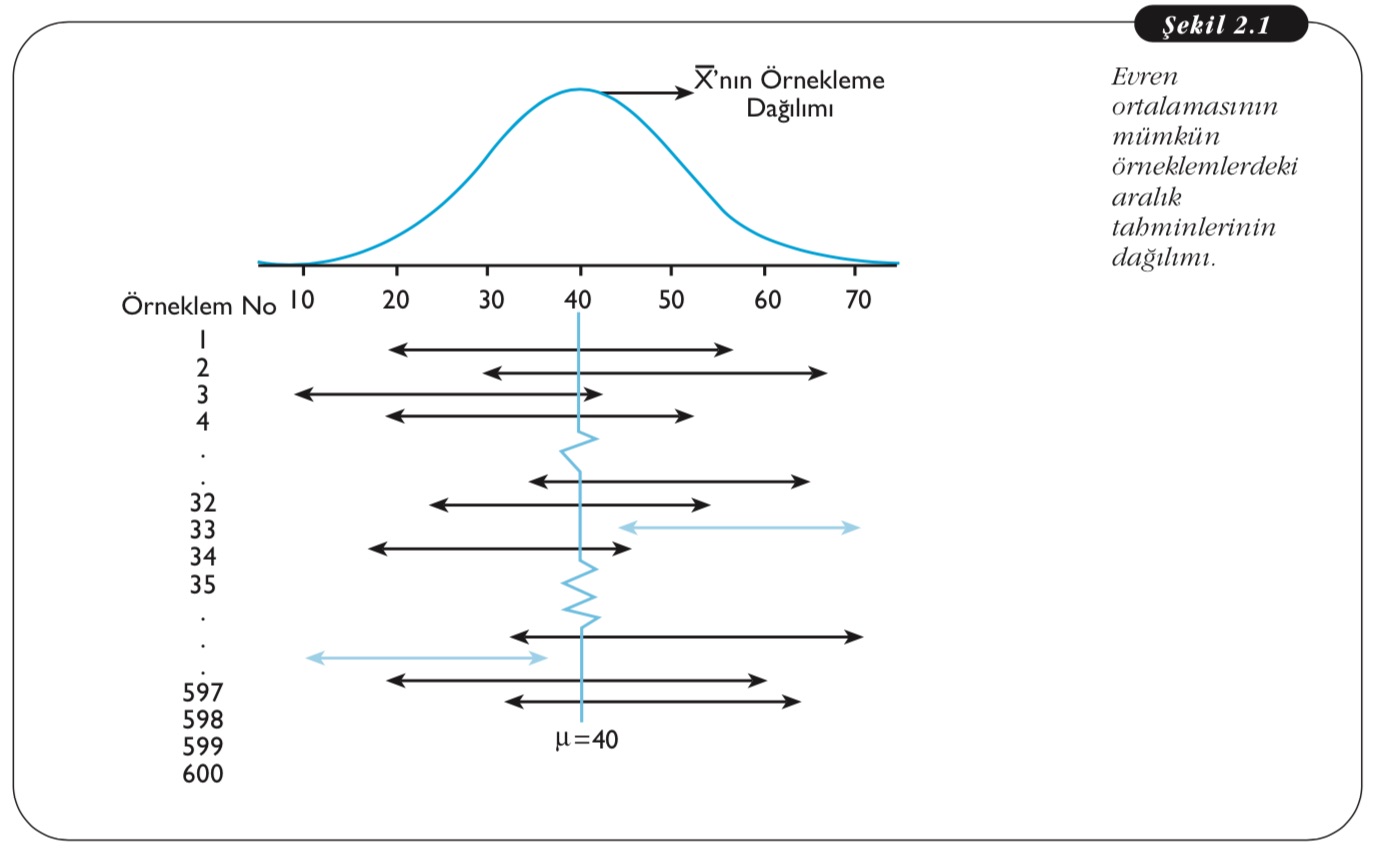
Güven düzeyi nedir?
Tahminleme sürecinde alt ve üst sınırlar birer rassal değişken, bu sınırların belirlediği aralık da rassal aralık niteliğindedir. Aralık tahminlemesi sürecinde, araştırmacı tarafından önceden belirlenen olasılık düzeyi ya da güven düzeyi (G.D.) parametre değerini kapsayan güven aralığının tahminlendiği olasılığı ifade eder ve 1-α ile gösterilir. Bir başka ifadeyle güven düzeyi tahminlenecek güven aralıklarının parametre değerini içine alma oranıdır. G.D.= 1-α değeri büyük seçilirse tahminlenen aralığın θ’yı kapsayan bir aralık olma olasılığı artmış fakat tahminlerin güvenilirliği, kesinliği azalmış olur.
Büyük örneklemlerde ana kütle ortalaması tahminlemesi için kullanılan eşitlikler ve bu eşitliklerin bileşenleri nelerdir?

Evren aritmetik ortalaması aralık tahminlemesinde evren standart sapması bilinmiyor ise ne yapılır?
Evren ortalaması aralık tahminlemesinde evren standart sapması kullanılan kısımlar örneklem standart sapması yardımıyla çözümlenir.t
Evren aritmetik ortalamasının aralık tahminlemesinde kullanılan bazı (1- α) değerleri için z (α/2) tablo değerleri nelerdir?
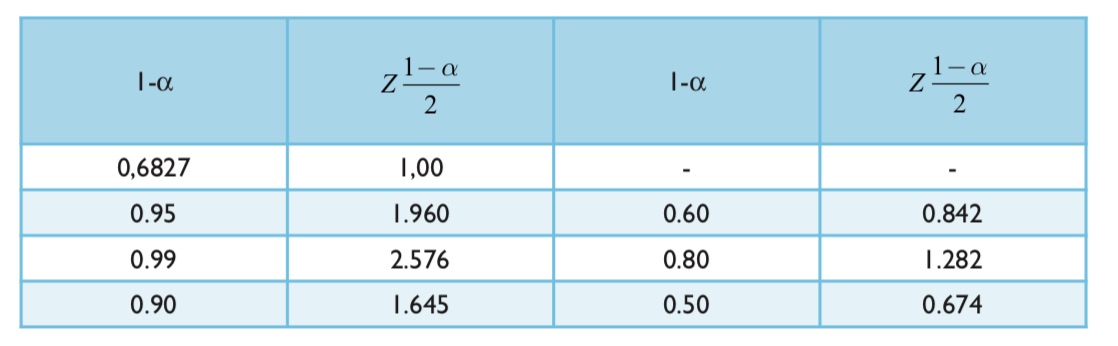
z ile gösterilen standart rassal değişken nasıl hesaplanır?
ilgili değer 0,3413'tür. Grafik yardımıyla görülebilir.