TÜREV VE UYGULAMALARI
Türev nedir?
Türev bir niceliğin bir başka niceliğe göre değişim oranını ifade eden kavramdır. Örneğin, hava sıcaklığının yere ve zamana göre değişimini; bir uçağın ya da otomobilin konumunun değişimini; elde edilecek gelirin üretilen mal miktarına göre değişimini; gök cisimlerinin birbirlerine göre konumlarının değişimini ifade etmek için türev kavramından yararlanmamız gerekir.
Ortalama hız nedir?
Ortalama hızı, alınan toplam yolun geçen toplam süreye oranı olarak tanımlanır. Bir doğru üzerinde hareket eden bir cismin kat ettiği yolu zamanın fonksiyonu olarak f (t) ile gösterirsek -ki buna konum fonksiyonu denir [t1, t2] gibi bir zaman aralığındaki ortalama hızı 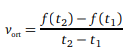 oranı ile hesaplanabilir.
oranı ile hesaplanabilir.
Konum fonksiyonu f(t) = 16t2 (metre) olan bir cismin [0,2] saniyelik zaman aralığındaki ortalama hızı ne olur?
f(t) = 16t2 fonksiyonu için 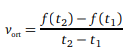 formülünde t1 = 0 ve t2 = 2 alırsak,
formülünde t1 = 0 ve t2 = 2 alırsak, ![]()
ortalama hız elde edilir.
f(x) fonksiyonunun x0 nokrasındaki limiti nasıl ifade edilir?
x değişkenini x0 dan farklı değerlerle, her iki yandan da x0 noktasına yeteri kadar yaklaştırdığımızda, f(x) fonksiyonunun alacağı değerler bir L sayısına yeteri kadar yaklaşıyorsa, o zaman bu L sayısına f(x) fonksiyonunun x0 noktasındaki limitidir deriz. Sembolik olarak ![]() gösterimi kullanılır.
gösterimi kullanılır.
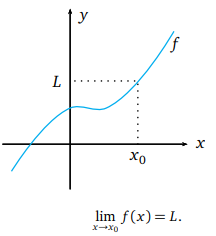
Bir x0 noktasına her iki yandan yaklaşmak ne demektir?
Bir x0 noktasına her iki yandan da yaklaşıyoruz dediğimizde hem x0’dan küçük değerlerle, hem de x0’dan büyük değerlerle yaklaştığımızı kastediyoruz. Ayrıca, fonksiyonun x0’da alacagı değerden ziyade, x0 noktasına çok yakın yerlerde alacağı değerler ile ilgilendiğimizden, fonksiyonun x0 noktasında tanımlı olması bile gerekli değildir. O yüzden de tanımı verirken x noktalarının x0 noktasından farklı olduğunu belirtiyoruz.
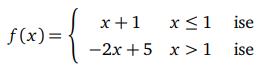
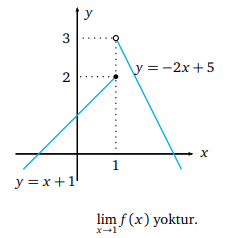
![]() nedir?
nedir?
Verilen örnek belli bir noktada limiti olmayan fonksiyon örneğidir. Fonksiyonun grafiği çizilirse, fonksiyonun sağdan yaklaşıldığında yaklaşık 3, soldan yaklaşıldığında 2 değerini aldığı gözlemlenir. Sağdan ve soldan limitleri farklı ise, limiti yoktur denir.
f(x) = x2 + x + 1 fonksiyonunun x0 = 2 noktasındaki limitini hesaplayalım.
Fonksiyonun grafiğinden de görüleceği gibi x sayısı 2 değerine yaklaşırken, fonksiyonun aldığı değerler de fonksiyonun x = 2 noktasında aldığı değere yani 7 sayısına yaklaşacaktır. 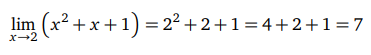
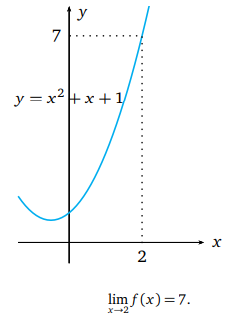
Türevin matematiksel tanımı nedir?
Bir x0 noktasını içeren bir aralıkta tanımlanan bir f (x) fonksiyonu verilsin. Eğer 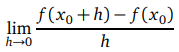 limiti varsa bu limit değerine f(x) fonksiyonunun x0 noktasında türevidir deriz. Türev için
limiti varsa bu limit değerine f(x) fonksiyonunun x0 noktasında türevidir deriz. Türev için ![]() gösterimlerinden biri kullanılabilir. Eğer fonksiyon tanım kümesi üzerindeki her noktada türevlenebiliyorsa, bu fonksiyona türevlenebilir fonksiyon denir.
gösterimlerinden biri kullanılabilir. Eğer fonksiyon tanım kümesi üzerindeki her noktada türevlenebiliyorsa, bu fonksiyona türevlenebilir fonksiyon denir.
Belirli bir x0 noktasındaki türevi nasıl tanımlarız?
Belirli bir x0 noktasındaki türevi şöyle de tanımlayabiliriz: 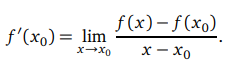
![]() sabit fonksiyonunun bir x noktasındaki türevi nedir?
sabit fonksiyonunun bir x noktasındaki türevi nedir?
Türevin değişim hızını ifade eder. x değişkeninde bir değişim olduğunda sabit fonksiyonun değerinde herhangi bir değişme olmadığından sabit fonksiyonun türevi sıfırdır.
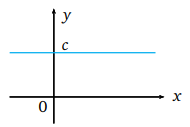
![]()
![]() fonksiyonunun türevi nedir?
fonksiyonunun türevi nedir?

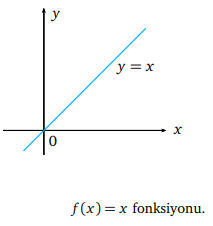
![]() ile verilen fonksiyonun türevi nedir?
ile verilen fonksiyonun türevi nedir?


Her sürekli fonksiyonun türevi var mıdır?
Sürekli fonksiyonlar, grafiklerini kalemimizi kağıttan hiç kaldırmadan çizebildiğimiz, diğer bir deyişle grafiklerinde herhangi bir kopma ya da sıçrama olmayan fonksiyonlardır.
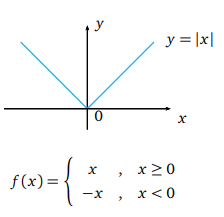
Dikkat ederseniz mutlak deger fonksiyonunun grafiğinde hiçbir kopma yoktur. Bu fonksiyon x = 0 noktasında süreklidir. Tanımı kullanarak türevine bakarsak, x=0 noktasında türevinin olmadığını görürüz.

Fonksiyonun grafiğine dikkat ederseniz x = 0 noktasında bir köşe yaptığını görürsünüz. İşte genel olarak fonksiyonların bu tür köşe noktalarında türevleri olmayacaktır. O halde her sürekli fonksiyonun türevlenebildiği yanılgısına düşmeyin.
f ve g fonksiyonları bir x noktasında türevlenebilsinler. Bu durumda bu iki fonksiyonun toplamının x noktasındaki türevi neye eşittir?
f ve g fonksiyonları bir x noktasında türevlenebilsinler. Bu durumda bu iki fonksiyonun toplamının x noktasındaki türevi, türevlerinin toplamına eşit olur
![]()
f(x) = x3 + x2 fonksiyonun türevi nedir?
Toplamın türevi, türevlerin toplamına eşit olduğundan,
![]() olarak bulunur.
olarak bulunur.
f ve g fonksiyonları x noktasında türevlenebilir ise f ve g fonksiyonlarının çarpımının türevi nedir?
Çarpımın türevi, türevlerin çarpımına eşit değildir ! “tesadüfler dışında!”
![]() (Birincinin türevi çarpı ikinci, artı ikincinin türevi çarpı birinci)
(Birincinin türevi çarpı ikinci, artı ikincinin türevi çarpı birinci)
c bir sabit olmak üzere c.f(x) çarpım fonksiyonunun türevi neye eşittir?
Bir fonksiyonun sabit sayıyla çarpımının türevi, türevinin aynı sabitle çarpımına eşittir.
![]()
h(x)=(2x−1)(x2 − 6x) çarpım fonksiyonunun türevi nedir?
Burada f(x) = 2x − 1 ve g(x) = x2 − 6x alabiliriz. h(x) = f (x) g(x) biçiminde olur ve çarpım kuralını hemen uygulanabilir.
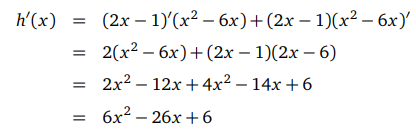
f ve g fonksiyonları x noktasında türevlenebilir olsunlar ve bölümden bahsedebilmek için g(x), sıfırdan farklı olsun.
O zaman (f/g)(x)'in türevi nasıl hesaplanır.
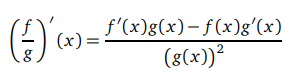 ile hesaplanır.
ile hesaplanır.
x satılan mal miktarını ve p fiyatını göstermek üzere, bu malın miktarı ve fiyatı arasındaki ilişki p = 200 − x ¸seklinde veriliyor.
Buna göre bu malın aylık gelir fonksiyonu R(x) = x · p = x(200 − x) = 200x − x2 şeklinde ifade ediliyor. Satılan mal miktarı x = 50 birimden x = 51 birime çıktığında gelirdeki değişim ne kadar olur?
R(51) − R(50)=(200 × 51 − 512) − (200 × 50 − 502) = 99 TL
Çözümün diğer bir yolu için, Türevin anlık değişimi verdiğini biliyoruz. O halde gelir fonksiyonumuzun x = 50 için türevini hesaplarsak
![]()
elde ederiz. Bu değer yukarıda hesaplanan değere oldukça yakındır ve yukarıda elde edilen deger yerine kullanılabilir. İktisadi uygulamalarda gelir fonksiyonunun türevine marjinal gelir fonksiyonu denir ve satılan mal miktarındaki bir birimlik artış için gelir fonksiyonundaki artışı (belki de azalışı) ifade eder. Gelirdeki degişimi hesaplamak için gelir fonksiyonunun türevinden yararlanırız
Eğimi m olan ve bir (x0, y0) noktasından geçen doğru denklemi nasıl ifade edilir?
Eğimi m olan ve bir (x0, y0) noktasından geçen doğru denklemi
y − y0 = m(x − x0) ile ifade edilir.

![]() parabolüne x = 1 noktasında teğet olan doğru denklemini yazalım
parabolüne x = 1 noktasında teğet olan doğru denklemini yazalım

İvme nedir?
Ilk defa Italyan Fizikçisi Galileo tarafından açık bir sekilde tarif edildigi bilinen ivme, belirli bir yönde hareket etmekte olan bir cismin
hızının belirli bir zaman aralıgındaki değişim miktarıdır. Başka bir deyişle ivme, bir cismin hızının değişim hızıdır.
Hızı, konum fonksiyonunun zamana göre değişimi, yani birinci türevi olarak tanımlanmıştı. Benzer bir yaklaşımla hızın zamana göre değişimini de hesaplayabiliriz. Elde edilen niceliğe ivme denir ve bu nicelik konum fonksiyonunun zamana göre ikinci mertebeden türevinden başka birsey değildir.
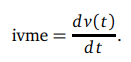
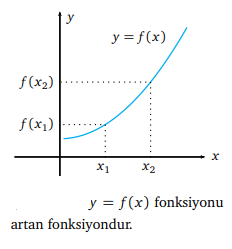
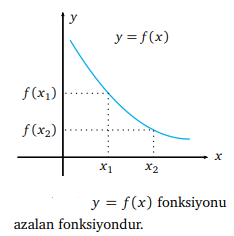
Artan ve azalan fonksiyon nedir?
Bir f (x) fonksiyonunun tanım kümesinden alınan keyfi x1, x2 noktaları için x1 < x2 iken f (x1) < f (x2) oluyorsa f (x) fonksiyonuna artan fonksiyon; eger, x1 < x2 iken f (x1) > f (x2) ise bu durumda da f (x) fonksiyonuna azalan fonksiyon denir.
R : [0, 200] → R, R(x) = 200x − x2 gelir fonksiyonunun artan ve azalan olduğu aralıkları bulalım.

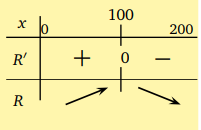
Bu bilgileri verilen tablo şeklinde de ifade edebiliriz. O halde gelirimiz satılan mal miktarı [0, 100] aralığında iken artmakta, [100, 200] aralığında iken azalmaktadır. Demek ki satış miktarı 100 birim olduğunda en çok gelir elde edilir