YÜZDE VE FAİZ HESAPLARI
Bir büyüklüğün %60’ı demek ne demektir?
Bir büyüklüğün %60’ı demek, eğer o büyüklük 100 birim olsaydı 60 birimi demektir.
%20 ifadesi ondalık olarak ne ifade eder?
%20 demek 0, 20 demektir.
Yüzdeler neyi ifade eder?
Yüzdeler büyüklük değil, yalnızca orandır. Yani bir büyüklügün ne kadarından bahsettiğimizi ifade eder.
Bir hisse senedinin değeri 100 TL’den 180 TL’ye yükseldiyse hissenin değeri yüzde kaç artmıştır?
Bir hisse senedinin değeri 100 TL’den 180 TL’ye yükseldiyse hissenin değeri, bağlı olarak 180−100/100 = 80/100 oranında artmıştır. İşte bu artışı %80 olarak gösteriyoruz.
%60 başka nasıl şekillerde ifade edilebilir?
3/5 kesirli sayısı hem "üç bölü beş" olarak hem de "beşte üç" olarak okunur. Bu kesri 20 ile genişletirsek 60/100 olur. İşte %60 budur.
12’nin %25’i nedir?
12’nin %25’i olan sayı (12× 25)/100 = 3’dür
50 sayısını %4 artırdığımızda yeni sayı ne olur?
50 + (50 × 4/100) = 52’dir
Haftalık harçlığı 50 TL olan bir çocuğun harçlığı %20 oranında azaltılırsa bu çocuğun haftalık harçlığı ne olur?
Harçlıgın azalma oranı %20 olduğunda, bunun harçlıkta meydana getirdiği mutlak azalma 50× 20/100 = 10 TL’dir. Yani yeni harçlık 50 − 10 = 40 TL olur.
an = 3n + 2 ¸seklinde verilen dizinin özelliği nedir, bu dizinin içinde yer alan terimlere örnek veriniz.
an = 3n + 2 ¸seklinde verilen dizi, ortak farkı 3 olan bir aritmetik dizidir. Bu dizinin ilk birkaç terimi
a1 = 3 · 1 + 2 = 5, a2 = 3 · 2 + 2 = 8, a3 = 3 · 3 + 2 = 11
an = 10n şeklinde verilen dizinin özelliği nedir ve dizide yer alan terimlere örnek veriniz.
an = 10n ¸seklinde verilen dizi de, ortak çarpanı 10 olan bir geometrik dizidir. Bu dizinin ilk bir kaç terimi
a1 = 101 = 10, a2 = 102 = 100, a3 = 103 = 1000
1 + 2 + 3 + ··· + 98 + 99 + 100 işleminin sonucu nedir?
Eğer bu toplamı ters sırada yazarsak 100+99+98+···+3+2+1 yine S olur, çünkü ters sırada yazmak toplamın degerini değiştirmez. Şimdi bu iki toplamı aşağıda görüldüğü gibi alt alta yazıp toplayalım.
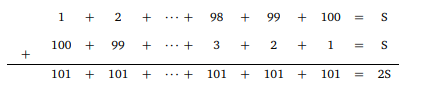
Görüldüğü gibi son satır 101’lerin toplamı oldu. Son satırda 100 tane 101 olduğundan 100 × 101 = 2S olur. Yani S = 100.101/2 = 5050 dir.
1+2+3+··· +n işlemi neye eşittir?
n(n + 1)/2
1+k+k2+···+kn işleminin sonucu neye eşittir?
(kn+1 − 1)/(k − 1)
Önümüzde bir tas çorba ve elimizde bir kaşık, bu çorbayı içmek istiyoruz; ama belli bir kuralla. Kural: içtigimiz her kaşık çorba bir önceki kaşığın yarısı kadar olacak. Yani ilk hamlemiz bir dolu kaşık, ikinci hamle yarım kaşık, üçüncü hamle 1/4 kaşık, dördüncü hamle 1/8 ve bu şekilde sürüp gidecek; bu tastaki çorbanın ne zaman biter?
Ilk hamlede 1 kaşık çorba içiyoruz.İkinci hamle sonunda 1 + 1/2 = 3/2 kaşık çorba içiyoruz. Üçüncü hamle sonunda 1 + 1/2 + 1/4 = 7/4 kaşık çorba içiyoruz. Bu şekilde n+ 1 hamle yaptığımızı düşünelim. n + 1’inci hamle sonunda,
1 + 1/2+1/4+1/8+ · ·+ 1/2 n
kaşık çorba içeriz. 1 + k + k2+ ··· + kn−1 = 1−kn /1-k olduğunu görmüştük.
Burada n yerine n + 1 alırsak,![]()
olur. Burada da k yerine 1/2 koyarsak,
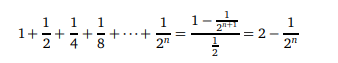
olur. Bu son elde edilen sayı da gördüğünüz gibi2’den küçüktür. Yani ne kadar uğraşsak da olur. 2 kaşık çorba bile içemeyiz.
Geçenlerde eşimle bir otomobil almak istedik, hatta birini beğendik, fiyatı da 30000 TL idi. Eşim ve ben ayda ancak 1000 TL biriktirebiliyoruz. Bir banka ayda %0, 50 faiz veriyormuş birikimlerimize. Biz her ay biriktirdiğimiz bu parayı o bankaya yatırsak ve aldığımız faizleri de üzerine eklesek kaç ay sonra o otomobili alacak paramız olur?
Bu yöntemle n ayda kaç lira biriktirebileceğimizi hesaplayalım. Başlangıçtaki 1000 liramız n ay sonra 1000·(1+0, 005)n olacak. 2’nci ay yatıracağımız 1000 lira ise n−1 ay bankada kalacagı için sonuçta 1000 ·(1+0, 005)n−1 liraya ulaşacak. 3’üncü ay yatıracağımız 1000 lira n−2 ay bankada kalacağı için sonuçta 1000 ·(1+0, 00)n−2 liraya ulaşacak. Bu şekilde devam edersek (n − 1)’inci ayda yatıracağımız para bir ay faizde kalacağı için 1000 ·(1+0, 005) lira olacak. Ve nihayet n’inci ayda da 1000 lira o ayın birikimi olarak elimizde olacak. Demek ki n ay sonra elimizde toplam,
1000 ·(1, 005)n + 1000 ·(1, 005)n−1 + ··· + 1000 · 1, 0050 + 1000
= 1000 · [(1, 005)n + (1, 005)n−1 + ··· + 1, 005 + 1] TL

Bankadan aylık %1, 37 faizle 5000 TL kredi aldığımızı varsayalım. Bu borcu da aylık 1000 TL eşit taksitlerle bankaya geri ödemek istersek ilk ay sonunda kalan para ne kadar olur?
Borcu aldıktan bir ay sonra aldığımız borç için aylık bir faiz uygulanacak ve bu faiz de 5000×0, 0137 = 68, 50 TL olacaktır. Aylık taksit 1000 TL’yi ödedikten sonra kalan borç miktarı 5068, 50−1000 = 4068, 50 TL olacaktır. Bankaya birinci ay için ödenen 1000TL’nin 68, 50 TL’si faiz ödemesi ve geri kalan 1000 − 68, 50 = 931, 50 TL’si ise anapara ödemesidir.

Bir arkadaşım bir bankadan ihtiyaç kredisi kullandı. Aldığı kredi miktarı 10000 TL, vadesi 24 ay ve aylık bileşik faiz %1, 27 idi. Buna göre arkadaşımın aylık taksidi ne kadar olacak?

%1, 14 faiz oranıyla 30000 TL kredi çekelim. Eger ayda 1000 TL taksitle bu borcu geri ödersek r = 0, 0114, B = 1000 ve A=30000 değerleri formülde yerlerine yazılırsa kaç ayda borç biter?

İtfa ne anlama gelir?
İtfa sözcügü günlük hayatta pek kullanılmamasına rağmen bundan türeyen itfaiye ne kadar yaygın bir kullanıma sahip. İtfa borcu söndürürken, itfaiye de yangın söndürüyor!
Borç amortismanı nedir?
Borç amortismanından kastımız, uygun bir faizle borç alınan bir paranın, taksitler
halinde geri ödenmesidir.