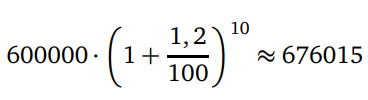ÜSTEL VE LOGARİTMİK FONKSİYONLAR
Başlangıçta 1 tane, bir gün sonra 2 tane, iki gün sonra 4 tane, üç gün sonra 8 tane. . . . olacak şekilde çoğalan nilüfer çiçekleri ile 15 gün sonunda gölün yarısını kaplıyorsa, çiçekler gölün tamamını kaç günde kaplar?

Her günün sonunda göldeki çiçeklerin sayısı iki katına çıkıyor. 15 gün sonra, gölün yarısı çiçeklerle kaplanıyorsa gölün yarısındaki çiçek sayısı 215 olur. Gölün tamamının kaplanması için gerekli çiçek sayısı 215 sayısının 2 katı olacaktır. Yani, 216. Gölü kaplayan çiçek sayısı 216 olduğuna göre 16. günün sonunda gölün tamamı dolacaktır
Üstel fonksiyon nedir?
a pozitif bir gerçel sayı ve a 1 olmak üzere f (x) = ax ¸seklinde tanımlanan fonksiyona üstel fonksiyon denir.
Üstel fonksiyon kavramını, polinom fonksiyon kavramıyla karıştırmayalım. Üstel fonksiyon tanımında x değişkeni üs’tedir.
f (x) = ax üstel fonksiyonunun tanım ve değer kümesi nedir?
Bu fonksiyonun tanım kümesi gerçel sayılar kümesidir; değer kümemizi de yine gerçel sayılar kümesi olarak alabiliriz. Biz daha çok a > 1 durumu ile ilgileneceğiz
f (x) = ax üstel fonksiyonunda a = 1 olursa ne olur?
Her x gerçel sayısı için ax = 1x = 1 olacağından bu fonksiyon sabit fonksiyona dönüşür.
f (x) = ax üstel fonksiyonunda neden a > 0 alınmaktadır?
Mesela a = −2 alamaz mıydık? (−2) sayısının tamsayı kuvvetlerini alabiliriz. Mesela, (−2)2 = 4,
(−2) 3 = −8 ¸seklinde tamsayı kuvvetleri anlamlıdır. Ancak herhangi bir gerçel sayı kuvvetini aldığımızda bu anlamlı olmayabilir. Örneğin, (−2) 1 /2 = olur. Ancak bir gerçel sayı degildir. Çünkü hiçbir gerçel sayının karesi −2 değildir.
f (x) = 2x ve g(x) = 10x fonksiyonlarının −1, 1, 2 ve 1/2 noktalarındaki görüntüleri nelerdir?
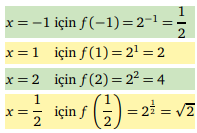
g(x) = 10x fonksiyonu için −1, 1, 2 ve 1/2 noktalarındaki görüntüleri
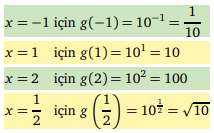
Her x gerçel sayısı için ax sayısı daima pozitif bir gerçel sayı olduğuna göre, x = 0 için ax kaçtır?
x = 0 için a0 = 1’dir.
a > 1 ve x’ler pozitif gerçel sayı ise ax hakkında ne söyleyebiliriz?

y = 2x üstel fonksiyonunda x’e negatif değerler verelim sonuç nasıl olur?
 gittikçe “0”’a yaklaşır
gittikçe “0”’a yaklaşır
a > 1 ve x negatif gerçel sayı ise; ax hangi sayılar arasında yer alır?
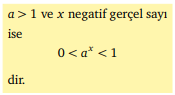
Üstel fonksiyonların özellikleri nelerdir?
Üstel fonksiyonların özelliklerini şu ¸şekilde sıralayabiliriz. a ve b pozitif sayılar, x ve y gerçel sayılar olmak üzere,
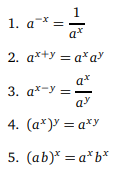
f(x) = 2x fonksiyonun grafiğini çiziniz
f (x) = 2x fonksiyonunda x’e bazı degerler vererek y değerlerini bulalım;

Bulduğumuz bu değerlerden faydalanarak, f(x) = 2x fonksiyonunun grafiğini çizebiliriz
Üstel fonksiyonun grafiği hep x ekseninin üstünde kalıyor. Ayrıca tüm grafikler hep (0, 1) noktasından geçiyor. Çünkü, her x gerçel sayısı için ax > 0 olduğundan üstel fonksiyonun grafiği, daima x ekseninin üstünde kalır. Ayrıca x = 0 değerine karşılık y = a0 = 1 değeri karşılık geldiğinden grafik daima (0, 1) noktasından geçmelidir.
f (x) = ax üstel fonksiyonunda a > 1 ise ax fonksiyonu nasıl fonksiyondur?
f (x) = ax üstel fonksiyonunda, a > 1 ise x1 < x2 için ax1 < ax2 olduğundan fonksiyon artan bir fonksiyondur.
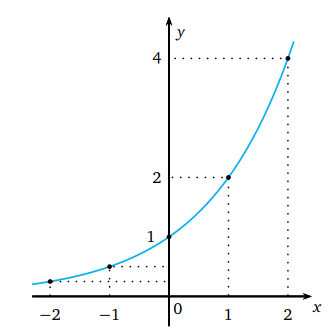
y = 2x , y = 3x ve y = 4x üstel fonksiyonlarının grafiklerini çiziniz.
f (x) = ax üstel fonksiyonun görüntü kümesi nedir?
Her x gerçel sayısı için ax > 0 oldugundan üstel fonksiyonun görüntü kümesi (0,∞) açık aralığıdır
Eğer fonksiyon grafiği veriliyorsa bu grafiğe bakarak fonksiyonun bire-bir mi örten mi olduğunu nasıl anlarız?
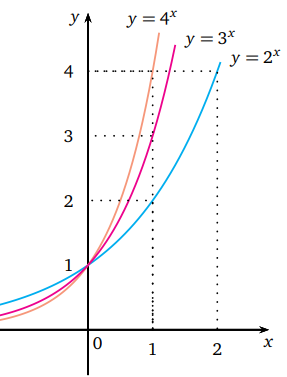
f : R → R fonksiyonunun grafiği verildiğinde, her y ∈ R noktasından x eksenine paralel olarak çizilen bir doğru, fonksiyonun grafiğini en fazla bir noktada kesiyorsa fonksiyon bire-birdir, en az bir noktada kesiyorsa fonksiyon örtendir.
Buna göre bizim tanımladığımız üstel fonksiyonlar bire-birdir.
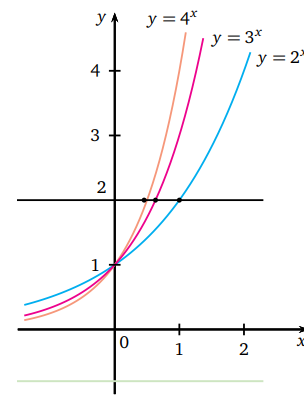
x eksenine paralel olarak çizilen bir doğru üstel fonksiyonun grafiğini en fazla bir noktada keser.
Üstel fonksiyonlar örten midir?
Değer kümesi olarak gerçel sayıları aldığımızda üstel fonksiyonlar örten olmaz. Örneğin, sıfır veya negatif sayılar, üstel fonksiyonun değeri olarak ortaya çıkmaz. Ancak değer kümesini pozitif sayılar olarak alırsak üstel fonksiyonlar örten olur.
Dolayısıyla üstel fonksiyonu bundan sonra f : R → (0,∞) f (x) = ax ¸seklinde fonksiyonlar olarak düşünecegiz.
(0,∞) aralığını R+ ile de gösteriyoruz. Bu şekilde düşündüğümüzde, üstel fonksiyonlar, bire-bir ve örten olur.
Bu sayede ax ’in ters fonksiyonunu tanımlayabileceğiz.
e harfi nedir?
e = 2, 7182818284590 ... ¸seklinde bir irrasyonel sayıdır. Bu e gösterimi, ilk kez ˙Isviçreli matematikçi Leonhard Euler tarafından 1727 yılında exponential kelimesinin ilk harfi e olduğu için kullanılmıştır. e sayısı da sonuçta bir sayıdır ve 2 ile 3 arasındadır.
2x = 16 eşitliği verildiğinde x değerini nasıl bulabiliriz?
2’nin hangi kuvvetini alırsak 16 eder sorusunun yanıtını aramalıyız. 2’nin 4. kuvveti 16 olacağından x sayısı 4 olmalıdır.
Logaritma fonksiyonu nedir?
Üstel fonksiyonların değer kümesini (0,∞) açık aralığı aldığımızda üstel fonksiyonların bire-bir ve örten fonksiyonlar olduğunu gördük. O halde f(x)=ax üstel fonksiyonunun ters fonksiyonundan bahsedebiliriz. İşte bu ters fonksiyona logaritma fonksiyonu diyeceğiz ve f −1(x) = loga x şeklinde göstereceğiz. Bu fonksiyonu kısaca y = loga x ¸seklinde de yazıyoruz.

y = 10x üstel fonksiyonunun ters fonksiyonu nedir?
y = 10x üstel fonksiyonunun ters fonksiyonu y = log10 x’dir.
Bayağı ve doğal logaritma nedir?
10 tabanına göre logaritmaya bayağı logaritma, e tabanına göre logaritmaya doğal logaritma denir.
25 = 32 olduğuna göre log2 32 kaçtır?
25 = 32 olduğuna göre log2 32= 5 dir.
Logaritma fonksiyonunun grafiği nasıldır?
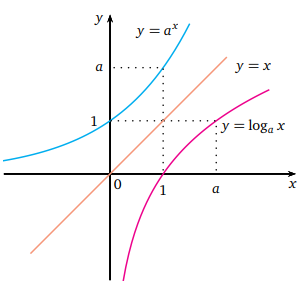
a > 1 için y = ax ve y = loga x fonksiyonlarının grafikleri.
Bir fonksiyonun grafiğini biliyorsak, ters fonksiyonunun grafiğini nasıl buluruz?
Bir fonksiyonun grafiğini biliyorsak, ters fonksiyonunun grafiğini bulabilmek için y = x doğrusuna göre yansımasını almak yeterlidir.
Örneğin; y=logex= lnx fonksiyonu tersi olan y=ex fonksiyonu grafiği
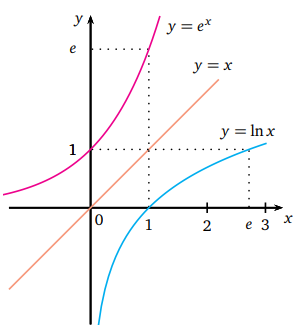
x ve y gerçel pozitif sayıları için, x ve y’nin çarpımının ve bölümünün logaritması nedir?
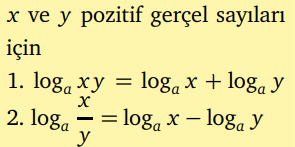
x ve y gerçel pozitif sayıları için, log x y nedir?
![]()
Bileşik faiz nedir?
Bileşik faiz, belirli zaman aralıklarında kazanılan faizin, anaparaya eklenmesiyle elde edilen tutarın faizidir.
Üstel ve logaritmik fonksiyonlar, bileşik faiz dışında, nüfus artışının hesabında da kullanılmaktadır. Belli bir zaman başlangıcında nüfus y0, birim zamandaki nüfus artış yüzdesi x olsun. t zaman sonra, başlangıçtaki nüfus ile nüfus artışının toplamı olan toplam nüfus yt olsun. Nüfus artışını,
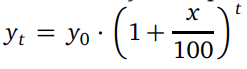 formülü ile hesaplayabiliriz.
formülü ile hesaplayabiliriz.
Maddenin başlangıçtaki kütlesi y0 olsun. t zaman sonra kalan kütle y(t) olmak üzere y(t)’yi nasıl buluruz?
y(t) = y0 · ek t formülüyle buluruz. Burada k, üstel azalış katsayısıdır.
Bizmut-210’un yarı-ömrü 5 gündür. Başlangıçtaki kütlesi 1600 miligram ise 3 hafta sonra kalan kütleyi bulabilir misiniz?
Yarı-ömür; maddenin yarısının bozunması için gereken süredir.
Başlangıçtaki kütlesi 1600 miligram ise y0 = 800’dür. Yarı-ömrü 5 gün olduğundan
y(5) = 1 /2 · 1600 = 800 olacaktır
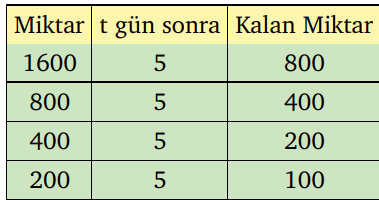
Yani, 1600 miligram Bizmut-210’un 20 gün sonra kalan kütlesi 100 miligramdır. 25 gün sonra 50 miligram kalacağına göre, 3 hafta da 21 gün olduguna göre. 100 miligramdan az 50 miligramdan fazla madde kalacaktır.
Başlangıçtaki nüfus y0 = 600000, artış yüzdesi x = 1, 2 olduğundan 10 yıl sonraki nüfus kaç olur?
Artış yüzdesi aynı olursa, 10 yıl sonra şehrin nüfusu;