FONKSİYONLAR
Fonksiyon nedir?
Boş kümeden farklı A ve B kümeleri alalım. A kümesinden B kümesine bir f fonksiyonu, A kümesinin her elemanına B kümesinin bir tek elemanını karşılık getirir. Burada A kümesine f fonksiyonunun tanım kümesi, B kümesine ise değer kümesi denir. A kümesinden B kümesine bir f fonksiyonu ![]() şeklinde gösterilir.
şeklinde gösterilir.
A: {1, 2, 3} kümesinden B: {a, b, c, d} kümesine iki adet f ve g fonksiyonlarını şema ile gösteriniz.
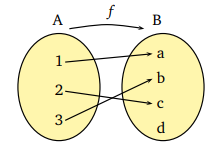
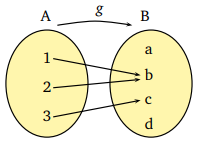
Burada A kümesi tanım kümesi, B kümesi değer kümesidir.
- Fonksiyonlarda Tanım kümesinde boşta eleman kalmaz, değer kümesinde boşta eleman kalabilir.
- Tanım kümesinde bir eleman değer kümesinde sadece bir eleman ile eşleşebilir.
A = {1, 2, 3} ve B = {a, b,c, d} kümeleri için, aşağıdaki eşleşmeler A kümesinden B kümesine neden birer fonksiyon olamaz?
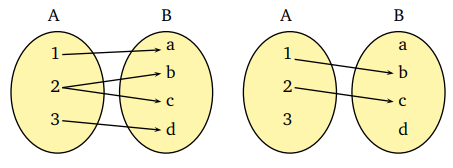

A kümesinin elemanı olan 2, B kümesinin hem b hem de c elemanıyla, yani birden fazla elemanıyla eşlendiğinden bir fonksiyon olamaz. Diğer eşlemede ise A kümesinin elemanı olan 3, B kümesinin hiçbir elemanıyla eşlenmemiştir. Bu yüzden bu eşlemeler fonksiyon olamaz.
- Fonksiyonlarda Tanım kümesinde boşta eleman kalmaz, değer kümesinde boşta eleman kalabilir.
- Tanım kümesinde bir eleman değer kümesinde sadece bir eleman ile eşleşebilir.
Fonksiyonunun görüntü kümesi nedir?..
f : A B fonksiyonu için, A kümesindeki elemanların f altındaki görüntülerinin oluşturduğu kümeye, f ’nin görüntü kümesi denir ve bu küme f (A) olarak gösterilir. O halde f ’nin görüntü kümesi,
f (A) = {f (a) | a A} kümesidir.
Sabit fonksiyon nedir?
f : A B fonksiyonu A kümesinin her elemanını B kümesinin aynı elemanı ile eşliyorsa f ’ye sabit fonksiyon denir. Yani c B olmak üzere, A kümesinden alınan her a elemanı için f (a) = c ise f ’ye sabit fonksiyon denir.
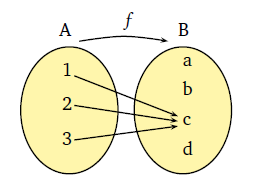
A = {1, 2, 3} kümesinden B = {a, b, c, d} kümesine bir sabit fonksiyon. (A’nın tüm terimlerini c’ye götürüyor)
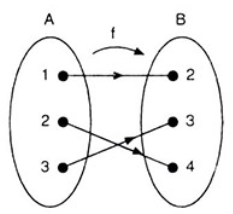
f : A → B fonksiyonu verilsin. f'ye ne tür fonksiyon denir?
f, bire-bir fonksiyondur.
f : A → B fonksiyonu verilsin. x1, x2∈ A olmak üzere x1 ≠ x2 iken f (x1)≠ f(x2) oluyorsa, buna denk olarak f (x1) = f (x2) iken x1 = x2 ise f’ye bire-bir fonksiyon denir.
Örten fonksiyon nedir?
f : A → B fonksiyonu verilsin. Her b ∈ B için f (a) = b olacak şekilde bir a ∈ A varsa, f fonksiyonuna örten fonksiyon denir. Ya da buna denk olarak, görüntü kümesi değer kümesine eşit olan fonksiyona, örten fonksiyon denir. Yani f : A → B fonksiyonu için f (A) = B ise f örtendir.
Eşit fonksiyon nedir?
f, g : A→ B fonksiyonları verilsin. Eğer tanım kümesinden aldığımız her a elemanı için, f (a) = g(a) oluyorsa, f ile g fonksiyonları eşittir.
Birim fonksiyon nedir?
f : A→ A fonksiyonu A kümesinin her a elemanını yine a ile yani kendisi ile eşliyor ise f ’ye A kümesinin birim fonksiyonu denir. Birim fonksiyon genelde f yerine I ile, veya tanım kümesini vurgulamak için IA ile gösterilir.
A = {1,2,3} kümesinin birim fonksiyonu; 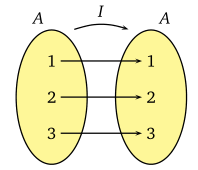
Ters fonksiyon nedir?
f : A → B, bire-bir örten bir fonksiyon olsun. Bu durumda, f fonksiyonunun ters fonksiyonu f−1ile gösterilir.
f−1: B → A fonksiyonu b ∈ B için f−1(b) = a olarak tanımlanır. Burada a, f (a) = b eşitliğini sağlayan yegane elemandır.
A = {1,2,3} kümesinden B = {x, y,z} kümesine 1-1 örten f fonksiyonu şekilde olduğu gibi verilmişse, f’nin ters fonksiyonu nedir?
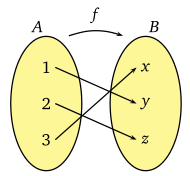
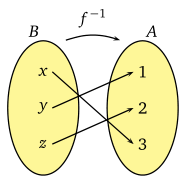
Bileşke fonksiyon nedir?
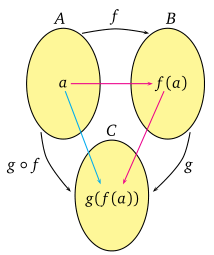
f : A → B, g : B → C fonksiyonları verilsin. Bu durumda g ◦ f : A→ C, (g ◦ f )(a) = g(f (a)) fonksiyonuna, f ile g fonksiyonunun bileşke fonksiyonu denir.
f :R →R , y = f (x) = x2+ x − 2 kuralı ile verilen fonksiyon için, x = 3’e karşlık gelen y = f (3) değerini bulunuz.
f (x) = x2+ x −2 ifadesinde, x gördüğümüz yere 3 yazarsak
f (3) = 32+3−2 = 9+3−2 = 10 olarak buluruz.
Mutlak değer fonksiyonu nedir?
Mutlak değer fonksiyonunu, parçalı tanımlı bir fonksiyon olarak ifade edebiliriz.
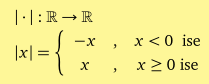
f : R →R
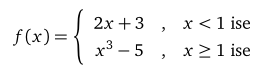
fonksiyonu için f (−2) ve f (2) nedir?
Fonksiyon, 1’den küçük olan bir x sayısını 2x + 3 sayısına; 1’e e¸sit ya da 1’den büyük olan bir x sayısını da x3−5 sayısına gönderiyor.
f(-2)’ yi bulalım. −2 sayısı 1’den küçük olduğundan (−2 < 1),
f (−2) = 2·(−2)+3 = −4+3 = −1 dir.
f (2)’yi bulalım. 2 sayısı 1’den büyük olduğundan (2 ≥ 1),
f (2) = 23−5 = 8−5 = 3 olur.
Fonksiyonlar da toplama, çıkartma, çarpma ve bölme işlemleri yapılabilir mi?

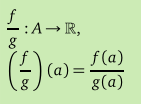 olarak tanımlanır.
olarak tanımlanır.
f, g : R → R, f (x) = x2+ 1, g(x) = x − 2 fonksiyonları için, f + g, f − g, f · g ve f / g fonksiyonlarını bulunuz.
Bu fonksiyonların her biri R’den R ye fonksiyonlardır.
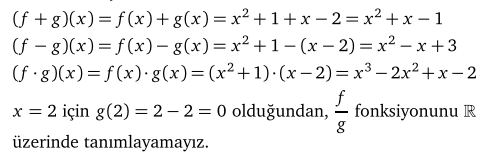
Polinom fonksiyon nedir?

![]()
Karekök içindeki ifadenin negatif olmaması gerekir. O halde x +1 ≥ 0 yani x ≥ −1 olmalıdır.
Dolayısıyla, Dg= [−1,∞).
f :R →R
f (x) = x +5 fonksiyonu örten midir?
Görüntü kümesi değer kümesine eşit mi yani? Bunun için değer kümesinden keyfi y elemanı alıp,
f (x) = y olacak biçimde x’in olup olmadığına bakacağız. Aldığımız keyfi y için bu özellikte bir x varsa, fonksiyon örtendir diyeceğiz.
y = x + 5 denkleminden x = y − 5 olur. Yani x = y − 5 için f (x) = y’dir. O halde, f örtendir.
![]()

Kartezyen koordinat sistemi nedir?

Kartezyen koordinat sistemi
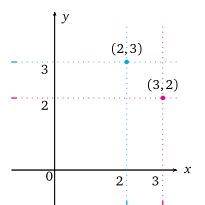
Kartezyen koordinat sisteminde (2,3) ve (3,2) ikililerine karşılık gelen noktalar nasıl gösterilir?
f : R→ R, f (x) = x − 2 fonksiyonunun grafiğini çizelim
x=0 için f(x)= y =-2……..(0,-2) noktası
y=0 için f(x)=0 ise; x=2….(2,0) noktası
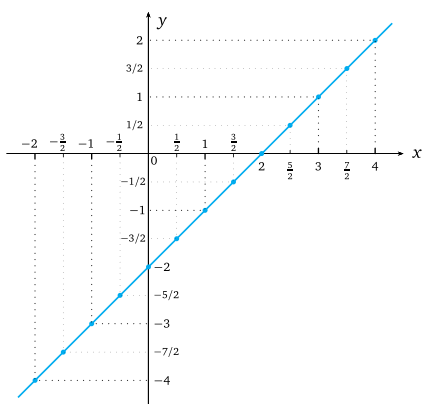 f (x) = x −2 fonksiyonunun grafiği.
f (x) = x −2 fonksiyonunun grafiği.
Thales Teoremi nedir?
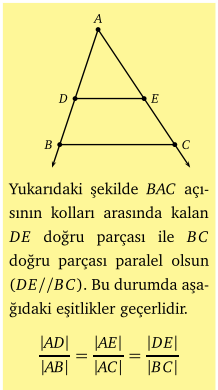
Doğrunun eğimi nedir?
Doğru üzerinde alınan farklı her hangi iki noktanın, ordinatları (y-ekseni) farkının apsisleri (x-ekseni) farkına oranı sabittir. Bu orana doğrunun eğimi diyoruz.

Doğrunun denklemi ve eğimi nasıl bulunur?

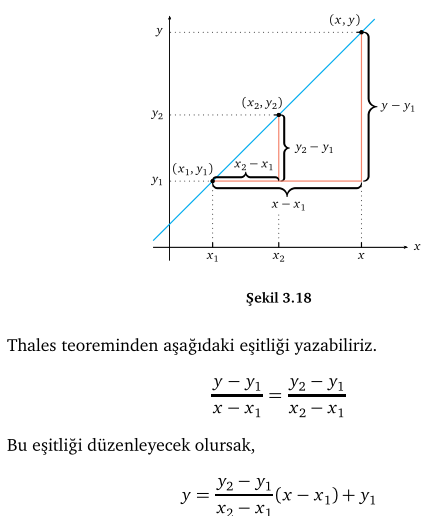

(1,2) ve (2,3) noktalarından geçen doğrunun denklemini bulalım.

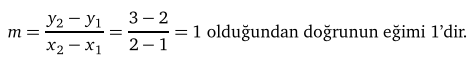
Düzlemde doğruların paralel olduğunu nasıl anlarız?