DENKLEMLER VE EŞİTSİZLİKLER
Cebirsel ifade ne demektir?
Bilinmeyen dediğimiz x, y,z,... gibi değişkenleri, 1,2,3,... gibi sayıları ve +, −, ×,..., kök alma gibi işlemleri içeren ifadelerdir. (cebirsel ifade eşitlik içermez).
Örneğin; 
2x – 1 ile x + 3 cebirsel ifadelerinin eşit olması durumunu düşünelim. 2x −1 = x +3 eşitliği x’in hangi değeri için doğrudur?
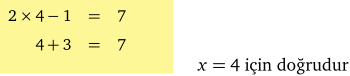
x = 4 değeri, 2x −1 = x +3 denkleminin çözümüdür.
Denklem, denklemin çözümü, çözüm kümesi, boş küme nedir?
Bilinmeyen içeren ve bilinmeyenin bazı değerleri için gerçeklenen eşitliklere denklem denir.
Bir denklemde eşitliği sağlayan bir sayıya, denklemin çözümü denir.
Denklemin çözümlerinin kümesine de çözüm kümesi denir.
Denklem bilinmeyenin hiçbir değeri için sağlanmıyorsa, çözüm yok ve çözüm kümesi boş kümedir denir.
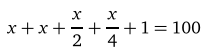denkleminin çözüm kümesi nedir?
bulunur.
Birinci dereceden bir bilinmeyenli denklem nedir?
Bir bilinmeyen içeren ve bilinmeyenin kuvveti bir olan denkleme, birinci dereceden bir bilinmeyenli (veya kısaca birinci dereceden) denklem denir.
Bu denklemlere örnek olarak,
3x +1 = 0,
2x −1 = x +5, ... gibi denklemler verilebilir.
İkinci dereceden bir bilinmeyenli denklem nedir?
Bir bilinmeyen içeren ve bilinmeyenin kuvveti iki olan bir denkleme, ikinci dereceden bir bilinmeyenli (veya kısaca ikinci dereceden) denklem denir.
(Tanım: a, b,c gerçel sayılar ve a 0 olmak üzere, ax2+ bx + c = 0 şeklindeki denklemlere ikinci dereceden bir bilinmeyenli denklemler denir.)
Bu denklemlere de örnek olarak,
x2+6x +9 = 0,
x2−3x +7 = 0, ... gibi denklemler verilebilir.
Genel olarak birinci dereceden bir bilinmeyenli denklemler nasıl gösterilir?
Genel olarak birinci dereceden bir bilinmeyenli denklemler a, b iki gerçel sayı ve a 0 olmak üzere,
ax + b = 0
şeklindedir. Bu tür denklemlerin çözümü eşitliği bozmayan işlemlerle kolayca çözülür.
Gökçe kardeşi ile babasından para istemiş. Baba, kardeşine parayı vermiş, Gökçe’ye de kardeşine verdiği kadar para vereceğini söylemiş, fakat Gökçe’yi meraklandırmak için, kardeşine verdiği parayı bulmasını istemiştir.
Kardeşi bu paranın beşte ikisine kot, dörtte birine kazak aldıktan sonra 35 lirası kaldığına göre, kardeşine verilen para kaç TL dir?
Önce probleme karşılık gelen denklemi yazmamız gerekiyor. Gökçe’nin babasının kardeşine verdiği paraya x dersek, denklemimiz;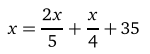
şeklinde olur. Bu denklemi çözüp, babasının verdiği parayı ve kot için harcanan parayı bulabiliriz.
100 TL babasının verdiği para.
Kotun fiyatı ise; 100 x (2/5) = 40 TL dır.
Dikdörtgen şeklindeki bir halının boyu, eninden 1 metre fazla ve halının alanı 6m2 ise; en-boy ölçüsünü bulmak için yararlanılacak denklem nasıldır?
Halının kısa kenarına x dersek, uzun kenarı x + 1 olur. Buradan,
x(x +1) = 6
x2+ x = 6
ya da
x2+ x −6 = 0 denklemi yazılabilir.
Özdeşlik nedir?
(x + y)2= x2+2xy + y2
(x − y)2= x2−2xy + y2
eşitlikleri herhangi iki x ve y gerçel sayıları için doğrudur. Böyle eşitliklere özdeşlik denir.
Diskriminant ∆(delta) nedir?
ax2+bx+c = 0 denklem çözümünde, b2−4ac ifadesine diskriminant denir ve ∆ = b2− 4ac’nin işaretine göre ikinci dereceden bir bilinmeyenli denklemin çözümü bulunur.
İkinci dereceden denklemin çözümü nasıl bulunur?
2x2− 3x + 1 = 0 denkleminin köklerini bulunuz.
Önce diskriminant ∆(delta)’yı bulalım
2x2− 3x + 1 ifadesinde a:2, b=-3, c=1 olduğundan,
Denklemde önce x=1 sonra x=1/2 yazılırsa; “0” eşitliği sağlanır.
2x2− 3x + 1 = 0
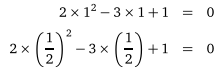
Birinci dereceden bir bilinmeyenli eşitsizlik nedir?
Eşitsizliklerin çözümü ile ilgili özellikler nelerdir?
- Bir eşitsizliğin iki tarafına aynı sayının eklenmesi veya iki tarafından aynı sayının çıkarılması durumunda eşitsizlik bozulmaz.
- Bir eşitsizliğin iki tarafının pozitif bir sayı ile çarpılması veya bölünmesi durumunda eşitsizlik bozulmaz.
- Bir eşitsizliğin iki tarafının negatif bir sayı ile çarpılması veya bölünmesi durumunda eşitsizlik yön değiştirir.
ax + b > 0 eşitsizliğinin çözüm kümesi nedir?
Eşitsizliğin her iki tarafına −b eklersek,
ax + b – b > 0− b
ax > −b buluruz.
−5x +3 > 0 eşitsizliğinin çözüm kümesini bulunuz.
−5x +3−3>0−3
−5x > −3
−5 negatif olduğundan, −5 ile böldüğümüzde eşitsizlik yön değiştirecek.
20 TL param var, bunun 10 TL sı ile kitap alacağım. Kalan para ile arkadaşlarıma çay ısmarlayacağım. Bir bardak çay 75 kuruş olduğuna göre, en fazla kaç kişiye çay ısmarlayabilirim?
Çay için 10 TL para kalıyor. Çay alabileceğimiz kişi sayısına x dersek, 75 kuruş da ¾ TL’ye denk olduğundan,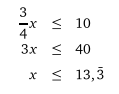
Eşitsizliğin çözümüne göre en fazla 13 kişiye çay ısmarlayabileceğim.
6x −18 ≤ 0 eşitsizliğinin çözüm kümesi nedir?
İkinci dereceden bir bilinmeyenli eşitsizlik nedir?
a, b,c gerçel sayılar, a 0 ve x herhangi bir gerçel sayı olmak üzere,
ax2+ bx + c > 0,
ax2+ bx + c < 0,
ax2+bx+c ≥ 0 veya
ax2+bx+c ≤ 0¸
seklinde yazılabilen eşitsizliklere ikinci dereceden bir bilinmeyenli eşitsizlikler denir. Böyle bir eşitsizliği sağlayan x değerlerinin kümesine de bu eşitsizliğin çözüm kümesi denir.
x2− x −2 > 0 eşitsizliğinin çözüm kümesi nedir?
Önce x2− x −2 ifadesini sıfır yapan değerleri bulalım. Yani, x2− x −2 = 0 denklemini çözelim.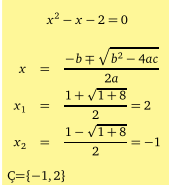 
Bu sayılar sayı doğrusunu üç aralığa ayırır. Bunlar, (−∞,−1), (−1,2) ve (2,∞) aralıklarıdır.
Bu aralıkların her birinde, x2− x −2 ifadesi ya hep pozitif ya da hep negatif değer alır. Denklem, -1 ve 2’nin dışında başka bir noktada sıfır değerini alamaz. Bu nedenle -1 ve 2 noktalarında x2− x −2 ifadesi, ya pozitif değerden negatif değere ya da negatif değerden pozitif değere geçer.
x2− x − 2’nin işaretini belirlemek istediğimiz aralıktan bir sayı seçeriz. Bu sayıyı, x2− x − 2 ifadesinde yerine yazarız.
Bulduğumuz değerin işareti x2−x−2’nin bu aralıktaki işaretidir. Çünkü bu aralıkta, x2− x −2 ifadesinin işaret değiştirmediğini biliyoruz.
Örneğin, -2’yi seçersek, x2− x −2 = (−2)2−(−2)−2 = 4+2−2 = 4, …… 4>0
1’i seçersek, x2− x −2 = (1)2−(1)−2 = 1−1−2 = −2,…… -2<0
3’ü seçersek, x2− x −2 = (3)2−(3)−2 = 9−3−2 = 4 …….. 4>0
Buluruz . Mavi ve Turuncu aralıklarda x2−x−2 ifadesi pozitif değer alır.
x2− x − 2 > 0 eşitsizliğinin çözüm kümesi; Ç=(−∞,−1)∪(2,∞).