KÜMELER VE SAYILAR
“Evrenin dili matematiktir” diyen bilin insanı kimdir?
Galileo “Evrenin dili matematiktir” demiştir.
Küme nedir?
İyi tanımlanmış nesneler topluluğuna küme denir. Kümeyi belirlerken, bir nesnenin o kümeye ait olup olmadığı, herkes tarafından net olarak anlaşılacak biçimde ifade edilmelidir.
Kümeler nasıl gösterilir?
Anlaşma kolaylığı açısından kümeleri A, B, C,... gibi büyük harflerle gösteriyoruz. Bir kümeyi oluşturan nesnelere kümenin elemanı denir ve kümenin elemanlarını da a, b,c,... gibi küçük harflerle gösterilir
Eğer a nesnesi A kümesinin bir elemanıysa bu durumu a ∈ A, eğer b nesnesi A kümesinin elemanı değilse bu durumu b A olarak gösterilir.
Bir kümeyi belirtmenin bir yolu elemanlarını { } biçiminde iki parantez arasına, aralarına virgül koyarak tek tek ifade etmektir. Bu gösterime “liste gösterimi” denir.
Örneğin bir, iki, üç ve dört sayılarından oluşan bir küme {1, 2, 3, 4} biçiminde gösterilir.
100’den küçük doğal sayılar kümesini liste gösterimi ile ifade ediniz.
Bu kümeyi {1, 2,... , 99} biçiminde ifade edebiliriz. Burada ilk birkaç eleman ile kümenin hangi elemanlardan oluştuğu anlaşılıyorsa geri kalan elemanları tek tek yazmak ˘ yerine “...” (üç nokta) ile ifade ediyoruz. Kümenin elemanları bir yerde son buluyorsa, son bir ya da birkaç elemanı da yazıyoruz.
Kümelerin “ortak özellik gösterimi” veya “kapalı gösterimi” nasıl ifade edilir?
Kümeyi oluşturan elemanları tek tek saymak yerine sağladıkları özelliklerle bu kümeye dahil edilmesine “ortak özellik gösterimi” veya “kapalı gösterim” denmektedir.
A= { x | x sayısı 100’den küçük doğal sayı}
Kümenin Venn şeması ile gösterimi nasıldır?
A = {1, 2, 3, 4} kümesini Venn ¸seması ile gösterebiliriz.
Sözkonusu problemde birden çok küme ile ilgileniliyorsa Venn şeması kullanılarak kümeler arasındaki ilişkiyi görmek kolaylaşmaktadır.
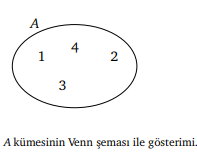
Altküme nedir? Nasıl gösterilir?
A ve B iki küme olsun. Her x ∈ A için x ∈ B ise A kümesine B kümesinin altkümesidir denir ve A ⊂ B ile gösterilir.
A = {1, 2} ve B = {1, 2, 3, 4} ise, A kümesi B kümesinin altkümesidir, A ⊂ B ile gösterilir
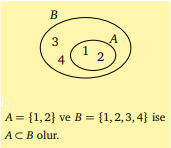
Alt kümenin Venn şeması ile gösterimi
Bir kümenin elemanlarının yazılışında sıranın değiştirilmesi ya da elemanların tekrar edilmesi kümeyi değiştirir mi?
Bir kümenin elemanlarının yazılışında sıranın değiştirilmesi ya da elemanların tekrar edilmesi kümeyi değiştirmiyor.
İki Kümenin eşitliği nasıl ifade edilir?
Eğer A ⊂ B ve B ⊂ A ise A ve B kümeleri eşittir denir ve A = B olarak gösterilir. A ve B kümelerinin eşit olmaması durumu da A B olarak gösterilir.
Örnek “LEBLEBİ” kelimesinin harfleri kümesi {B, E, İ, L} olur. Bu küme aynı zamanda “BELLİ” kelimesinin harfleri kümesine de eşittir.
A kümesinin elemanları A={a,b,c} olarak verilmişse; seçeneklerden hangisi A kümesinin öz altkümesi değildir?
A ⊂ B ve A ≠ B ise A kümesi B kümesinin öz altkümesidir denir.
Yani A kümesinin kendisi dışında olan alt kümeleri öz altkümelerini oluşturur.
A kümesinin alt kümeleri; { }, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a, b, c} dir.
Alt küme sayısı; kümede olan terim sayısı n olmak üzere 2n ile verilir. Soruda 23 =8 tane alt kümesi var. Öz altküme sayısı 2n -1 sayısı kadardır.
Kendisi olan alt küme {a, b, c} olduğu için geriye kalanlar öz altkümeyi oluşturur.
Boş küme nedir?
Hiçbir elemanı olmayan kümeye boş küme denir. Boş küme ![]() simgesiyle gösterilir.
simgesiyle gösterilir.
A herhangi bir küme olmak üzere ![]() ⊂ A olur.
⊂ A olur.
A = {1, 2} kümesinin tüm alt kümelerini sayabilir misiniz?
![]() , {1}, {2}, {1, 2}
, {1}, {2}, {1, 2}
A kümesinden herhangi bir eleman seçtiğimizde bu eleman yine A kümesine ait olduğundan A kümesi kendisinin alt kümesidir.
Evrensel küme nedir?
Herhangi bir problemle ilişkili tüm kümeleri kapsayan kümeye “evrensel küme” diyoruz. Evrensel küme genel olarak E ile gösterilir. Evrensel küme seçilen probleme göre değişebilen bir kümedir.
Örneğin; yalnız 10’dan küçük doğal sayıları kullanacaksak E = {1, 2,... , 9} olarak belirlemek yeterlidir
E = {1, 2,... , 9}, A = {2, 4, 6} ve B = {6, 7, 9} ise Venn şeması nasıl olur?
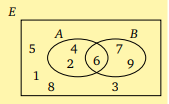
Kümelerin birleşimi nedir?
A ve B kümelerinden en az birine ait elemanların oluşturduğu kümeye A ve B kümelerinin birleşimi denir ve A∪ B ile gösterilir. Bir başka deyişle,
A∪B = { x| x ∈ A veya x ∈ B} olur.
A = {2, 4, 6} ve B = {6, 7, 9} için A∪ B = ?
Küme birleşiminde Hem A kümesi hem de B kümesinde bulunan terimler birer kez yazılır
A∪ B = {2, 4, 6, 7, 9} olur.
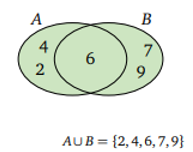 birleşim kümesinin Venn şeması ile gösterimidir.
birleşim kümesinin Venn şeması ile gösterimidir.
Keyfi A, B, C kümeleri için birleşim ile ilgili hangi özellikler geçerlidir?
Keyfi A, B, C kümeleri için birleşim ile ilgili şu özellikler geçerlidir.
- A∪ B = B ∪ A (Değişme özelliği)
- A∪ (B ∪ C)=(A∪ B) ∪ C (Birleşme özelliği)
- A∪ = A ve A∪ E = E
- A ⊂ A∪ B ve B ⊂ A∪ B
Boş küme eleman içermediğinden A kümesi ile birleşimi A olacaktır.
Evrensel küme, ilgili probleme ait tüm kümeleri içerdiğinden A kümesi ile birleşimi yine evrensel küme olacaktır.
A= {1,2}, B = {2,3}, ve C = {3,4} kümeleri için (A∪ B)∪ C ve A∪(B ∪ C) küme birleşimlerinin eşit olduğunu gösterelim
A∪ B = {1,2,3},
B ∪ C = {2,3,4},
(A∪ B)∪ C = {1,2,3,4}
ve
A∪(B ∪ C) = {1,2,3,4} olur.
İki kümenin kesişimi nedir?
Hem A hem de B ye ait elemanların oluşturduğu kümeye A ile B nin kesişimi denir ve A∩ B ile gösterilir.
Bir başka deyişle; A∩ B = {x| x ∈ A ve x ∈ B} olur.
A = {2, 4, 6} ve B = {6, 7, 9} kümeleri için kümelerin kesişimi A∩ B = ?
A = {2, 4, 6} ve B = {6, 7, 9} kümeleri için A∩ B = {6} olur.
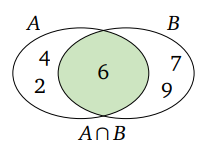
Keyfi A, B, C kümelerinin kesişimi ile ilgili özellikler nelerdir?
keyfi A, B, C kümeleri için kesişim ile ilgili şu özellikler doğrudur.

A fark B kümesi A\ B nedir?
A’ya ait olan ancak B’ye ait olmayan elemanların kümesine A fark B kümesi denir ve bu küme A\ B ile gösterilir.
A\ B = {x| x ∈ A ve x ![]() B} Benzer olarak
B} Benzer olarak
B \ A = {x| x ∈ B ve x ![]() A}
A}
A = {1, 3, 5} ve B = {1, 2, 3, 4} kümeleri için, AUB, A∩B, A\B, B\ A nedir?
A = {1, 3, 5} ve B = {1, 2, 3, 4} kümeleri için
A∪ B = {1, 2, 3, 4, 5}
A∩ B = {1, 3}
A\ B = {5} ve (A kümesinde olup, B kümesinde olmayan)
B \ A = {2, 4} olur (B kümesinde olup, A kümesinde olmayan)
A = {1, 2, 3} ve B = {4, 5, 6} kümeleri için A∩ B=?, A∪ B =?
A = {1, 2, 3} ve B = {4, 5, 6} kümeleri için
• A∪ B = {1, 2, 3, 4, 5, 6}
• A∩B =![]() olur, çünkü hem A hem de B kümesine ait olan eleman yoktur
olur, çünkü hem A hem de B kümesine ait olan eleman yoktur
Ayrık küme nedir?
Ortak elemanları olmayan, bir başka deyişle kesişimleri boş olan kümelere “ayrık kümeler” denir.
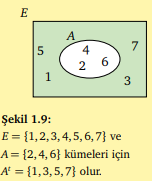
Bir kümenin evrensel kümeye göre tümleyeni nasıl tanımlanır?
E evrensel kümesi ve bunun bir A altkümesi verilsin. E kümesine ait olup A kümesine ait olmayan elemanların kümesine A kümesinin E kümesine göre tümleyeni denir ve bu küme At ile gösterilir.
E = {1, 2, 3, 4, 5, 6, 7} ve A = {2, 4, 6} kümeleri için At = {1, 3, 5, 7} olur.
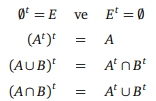 olduğu söylenebilir.
olduğu söylenebilir.
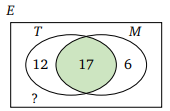
45 kişilik bir sınıfta belli bir sınav döneminde Türkçe dersinden başarılı olanlar 29 ve Matematik dersinden başarılı olanlar 23 kişidir. Her iki dersten başarılı olanlar 17 kişi olduğuna göre her iki dersten de başarısız olan kaç kişi vardır?
Türkçe dersinden başarılı olan öğrencilerin kümesini T, Matematik dersinden başarılı olan öğrencilerin kümesini M ile isimlendirelim. Her iki dersten başarılı olan öğrenciler T ∩M kümesini oluşturur. Her iki dersten de başarısız öğrenciler T ∪ M kümesinin tümleyenine aittir. Bu kümede kaç öğrenci olduğunu bulmak istiyoruz.
Kesişim kümesinde 17 kişi olduğuna göre T \M, yani yalnızca Türkçe dersinden başarılı öğrencilerin kümesi 29 − 17 = 12 kişidir. M\T yani yalnızca Matematik dersinden basarılı öğrencilerin kümesi de 23 − 17 = 6 kişidir.
Bu derslerin herhangi birinden başarılı öğrencilerin kümesi T ∪ M olur ve bu kümenin 12 + 17 + 6 = 35 elemanı vardır. Sınava giren 45 öğrenci, en az bir dersten baş¸sarılı 35 öğrenci olduguna göre, her iki dersten başarısız olan öğrenci sayısı 45 − 35 = 10 olur.
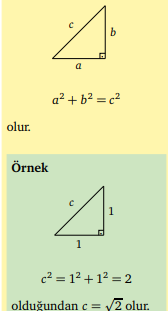
Pisagor Teoremi nedir?
Pisagor Teoremi: Bir dik üçgende iki dik kenarın uzunluklarının kareleri toplamı, hipotenüsün karesine eşittir. Yani a, b,c üçgenin
kenar uzunlukları olmak üzere
Üslü sayıların özellikleri nelerdir?
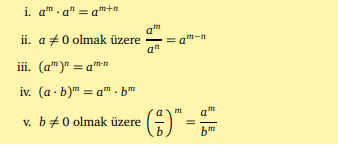
a sayısının n. dereceden kökü nasıl ifade edilir?

Üslü sayılar, köklü olarak nasıl ifade edilir?
