Diziler ve Seriler
Dizi ve serinin tanımları nelerdir?
Bir dizinin, sonsuz sayıda sıralı terimden oluştuğunu var sayıyoruz. Seri ise sonsuz sayıda terimin toplamı şeklinde tanımlanıyor.
Birkaç dizi örneği veriniz.
Fibonacci dizisi nedir?
a1 = 1, a2 = 1, a3 = a1 + a2, a4 = a2 + a3, ..., an+2 = an + an+1, ...
Bu diziye Fibonacci dizisi denir. Bu şekilde tanımlanmış dizilere, yani belli bir terimden sonraki elemanlarının, daha önceki elemanlar cinsinden tanımlandığı dizilere tekrarlamalı diziler denir.
Bir {an} dizisi için a ve n'nin farklı değerleri için sonuçları değerlendiriniz.
{(—1)n} = {—1, 1, —1, 1, ...} dizisini yorumlayınız.
{(—1)n} = {—1, 1, —1, 1, ...}dizisi dönüşümlü ve sınırlı bir dizidir, bütün terimleri
alttan -1, üstten ise 1 ile sınırlıdır fakat monoton bir dizi değildir
Bir dizinin limiti ne anlam ifade eder?
an = 1/n dizisinin limitinin sıfır olduğunu gösteriniz.
Limitin temel özellikleri nelerdir?
limitini hesaplayınız.
limitini hesaplayınız.
Dizilerin yakınsak ya da ıraksak olması neye bağlıdır?
a) {an} artan ve üstten sınırlı bir dizi ise, yakınsaktır.
b) {an} azalan ve alttan sınırlı bir dizi ise, yakınsaktır.
c) {an} artan ve üstten sınırlı değilse, ıraksaktır.
d) {an} azalan ve alttan sınırlı değilse, ıraksaktır
Serilere örnek veriniz.
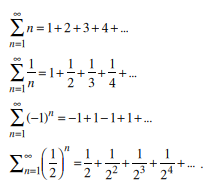
Serinin yakınsaklığı neyi ifade eder?
Bir seri hangi durumlarda yakınsak ya da ıraksaktır?
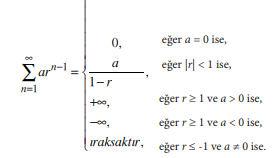
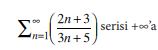yakınsar mı uzaksar mı?
çünkü 
Bölüm kuralı neyi ifade eder?
Mutlak yakınsaklık neyi ifade eder?
Şartlı yakınsak ne anlama gelir?
serisi yakınsak olup fakat mutlak yakınsak değilse bu seriye şartlı yakınsak
seri denir.
Dönüşümlü seriler için yakınsaklık kuralları nelerdir?
serisinin yakınsaklık durumunu inceleyiniz.
